|
Wszystkie rysunki utworzono za pomocą programu C.a.R. Można przesuwać 'wypełnione' punkty. |
Na lekcji pani podała, jak znaleźć konstrukcyjnie punkt P' stanowiący odbicie punktu P w prostej m:
- na m zaznaczamy punkt Pm leżący najbliżej P,
- rysujemy okrąg o środku Pm przechodzący przez P,
- P' jest punktem przecięcia okręgu z prostą PPm (różnym od P).
Na rysunku można obejrzeć tę konstrukcję dla punktów P, Q i T.
Karol, jak to Karol, niby słuchał uważnie, jednak omyłkowo przyjął, że
Na rysunku można obejrzeć tę konstrukcję dla punktów P, Q i T.
Sprawdź, że wszystko się zgadza! Mamy bowiem:
- Pm jest punktem z m leżącym w najmniejszej odległości od punktu P,
- zaznaczony jest okrąg o środku Pm przechodzący przez P,
- P' jest punktem przecięcia okręgu z prostą PPm (różnym od P).
Nazwijmy to przekształcenie emsymetrią, albo m-symetrią.
Zbadamy, jakie ma ono własności. W szczególności jak wyglądają obrazy odcinków i okręgów w m-symetrii.
Podstawowe własności m-symetrii zebrane są w poniższym zadaniu.
|
Wprowadźmy oznaczenia:
P' - obraz punktu P w m-symetrii, P'' - obraz punktu P' w m-symetrii, o(S, r) - okrąg o środku S i promieniu r, a - prosta prostopadła do AB, przechodzącą przez A, b - prosta prostopadła do AB, przechodzącą przez B. |
Zadanie 1. Uzupełnij.
a) Jeśli P 
m, to P' = . . . . . ..
b) Jeśli P' = P, to P . . . . . ..
c) P'
m wtedy i tylko wtedy, gdy P . . . . . ..
d) P'' = P' wtedy i tylko wtedy, gdy P . . . . . ..
e) P'' = P wtedy i tylko wtedy, gdy P . . . . . ..
f) Obrazem okręgu o(S, r) jest półokrąg wtedy i tylko wtedy, gdy S . . . . . . .
g) Obrazem o(S, r) jest okrąg wtedy i tylko wtedy, gdy . . . . . ..
h) Gdy odcinek KL nie przecina ani . . . . . ., ani . . . . . ., jego obrazem jest odcinek.
i) Gdy KL || AB, to obraz KL jest . . . . . ..
j) Obraz odcinka KL jest odcinkiem wtedy i tylko wtedy, gdy . . . . . ..
Jeśli Karol mógł coś przekręcić, to my też. Przyjmijmy, że
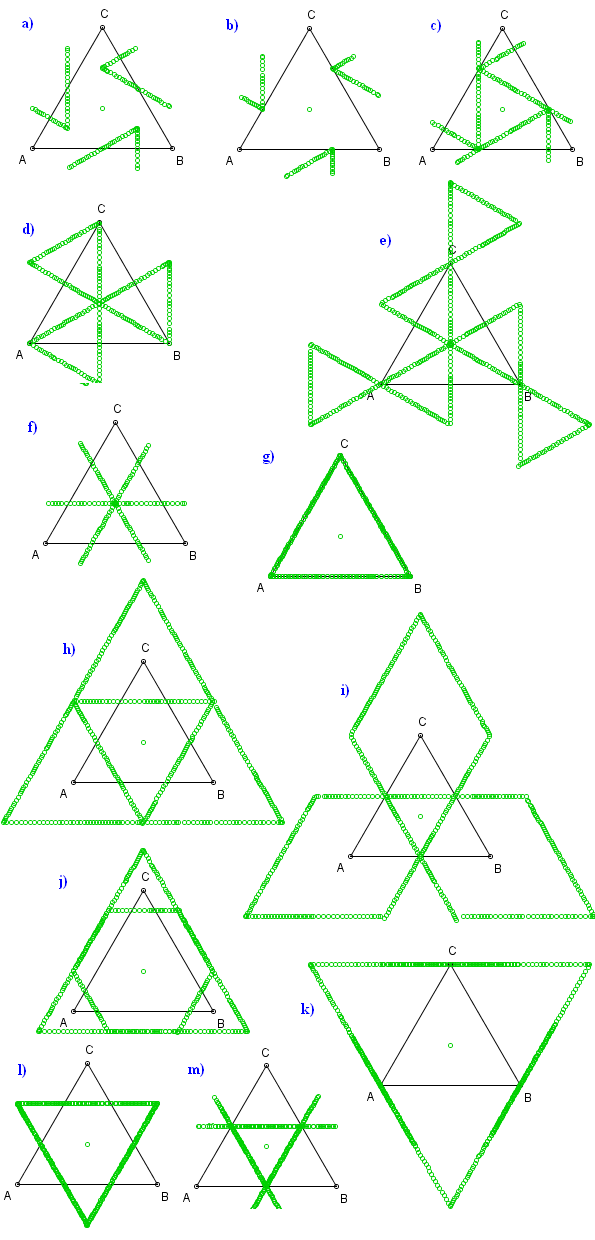
Jak wyglądają obrazy odcinków i okręgów? Zobacz.
Zauważ, że gdy przemieszczamy punkt P (albo Q lub T), jego obraz P' czasami gwałtownie zmienia pozycję, dokonuje 'skoku'.
Nie obserwujemy tego zjawiska, gdy P przesuwamy poza obszarem kąta (wypukłego) ABC. Może się wydawać, że 'skoki' punktu P' zachodzą w sytuacji, gdy P przechodzi w pobliżu dwusiecznej kąta ABC.
Powodem tych 'skoków' jest... dziedzina m-symetrii.
Istnieją takie położenia punktu P, dla których są dwa najbliższe punkty Pm, tzn. na łamanej są dwa punkty w najmniejszej odległości od P. Wtedy określenie punktu P' nie jest jednoznaczne. Takie punkty P nie należą do dziedziny tego przekształcenia.
Dokładniej, gdy m jest łamaną ABC, to dziedziną m-symetrii są wszystkie punkty płaszczyzny z wyjątkiem punktów leżących na:
- fragmencie dwusiecznej kąta ABC,
- fragmencie (półprostej) symetralnej odcinka AC,
- fragmencie paraboli o ognisku O i kierownicy k.
Zobacz.
Zadanie 2. Niech m będzie łamaną ABC.
Gdy . . . . . . , to dziedziną m-symetrii jest płaszczyzna bez punktów dwusiecznej kąta ABC.
Ciekawie jest, gdy przyjmiemy, że
Jak wyglądają obrazy odcinków i okręgów? Zobacz.
Zadanie 3. Opisz dziedzinę m-symetrii, gdy m jest łamaną zamkniętą ABCA.
Gdy m jest brzegiem trójkąta równobocznego ABC, to obrazy okręgów, o środku O w środku trójkąta, przyjmują dość regularne kształty. Zobacz.
Zadanie 4. Poniżej widać obraz okręgu o(O, r), gdzie O jest środkiem trójkąta równobocznego ABC, o boku a = 4. Naszkicuj ten okrąg i wyznacz dokładną wartość r.
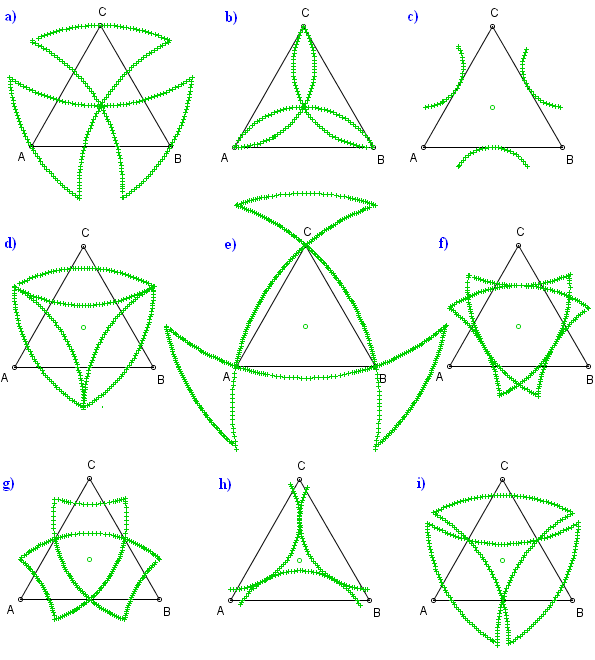
Niech m będzie brzegiem trójkąta równobocznego ABC o boku 4. Obrazy brzegów trójkątów równobocznych DEF o środku O w środku trójkąta ABC przyjmują dość regularne kształty. Zobacz.
Zadanie 5. Poniżej widać obraz brzegu trójkąta równobocznego o boku b, o środku O w środku trójkąta ABC (o boku a = 4). Naszkicuj brzeg tego trójkąta i wyznacz dokładną wartość b.
Ciekawie jest, gdy przyjmiemy, że
Zadanie 6. Opisz dziedzinę m-symetrii, gdy m jest brzegiem kwadratu ABCD.
Zobacz, jak wyglądają obrazy brzegów kwadratów EFGH o środku w środku kwadratu ABCD.
