Jak zbudować optymalne pudełko?
Zapewne każdy nauczyciel i niejeden maturzysta kojarzy z tym pytaniem
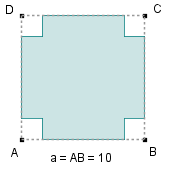
rysunek taki, jak obok i zadanie:
Zadanie 1.
Jakie wymiary ma pudełko o największej objętości,
o podstawie kwadratowej, otwarte z góry, utworzone z kwadratu o boku a = 10 cm ?
Jak omówić to z uczniami?
Przyjrzyjmy się temu bliżej, omówimy różne sposoby prezentacji.
Gdy x oznacza długość boków usuwanych kwadratów, to jest to wysokość pudełka,
a jego podstawa ma pole (10 - 2x) 2.
Zatem wystarczy zbadać funkcję f (x) = (10 - 2x) 2 . x.
Może zamiast badać funkcję, wystarczy oglądnąć jej wykres?
(Wtedy będzie to dostępne nie tylko dla znających pochodne.)
Takie podejście ma wady:
- wykres f jest bardzo 'ciasny' (może lepiej użyć pomocniczej funkcji
g?),
- to komputer (a nie uczeń) postawił kropkę, znalazł ekstremum funkcji,
- trudne jest ułożenie wzoru funkcji, co zostału tu zignorowane,
- i jeszcze drobiazgi: dlaczego takie oznaczenia, dlaczego f, a nie V,
dlaczego x, a nie h ?
Może zrobić rysunek w programie CaR?
Można przesuwać punkt P.
Zwykła kartka papieru i nożyczki dadzą lepszy efekt; można na oczach dzieci zaginać kartkę tak, by zobaczyli pudełko. (Bez nożyczek też można - można wydzierać narożniki.)
Jednak jest pewna korzyść z komputera, przesuwając P, widać wiele możliwych pudełek.
Przy jakim położeniu jest największa objętość? O, to jest pytanie (= zadanie).
Na szczęście w programie CaR można (na oczach widzów):
- zaznaczyć czworokąt podstawy i nazwać go podstawa ,
- zaznaczyć odcinek AP i nazwać go h ,
- wstawić wyrażenie arytmetyczne o nazwie V i określić
jego wartość: podstawa * h
(w CaRze nazwy są zarazem zmiennymi o wartościach: pole i długość).
Można przesuwać punkt P.
Przesuwając punkt P i oglądając V odnajdziemy (doświadczalnie) takie h, przy którym objętość V jest największa.
Tu jednak komputer też dużo zrobił sam, czy nie za wiele?
Może warto skorzystać z arkusza kalkulacyjnego takiego jak poniżej?
(Poniżej możesz zmieniać liczby w zielonych okienkach).
a =
h0 =
![]() h =
h =
| h | a - 2*h | (a - 2*h)^2 | (a - 2*h)^2 * h |
Aby arkusz zadziałał, należy go zaprojektować, czyli oprócz wymyślenia formuł takich, jak w nagłówkach kolumn, trzeba jeszcze je przełożyć na język arkusza. Zatem wysiłek idzie 'w klawisze'.
A przecież, by wypełnić taką tabelę, nie jest potrzebny komputer.
Wystarczy na tablicy zacząć wypełniać tabelę taką, jak poniżej.
Nie zaczynałbym od h = 0, nie ma potrzeby nad tym się rozwodzić.
Warto obgadać zera pojawiające się dla h = 5.
(Bez mówienia o dziedzinie funkcji! Nie jest konieczne używanie słowa 'funkcja'.)
Dalej planujemy zagęszczanie, czyli wartości h dla dalszych wierszy
(i wtedy jest miejsce na kalkulator).
| h | bok podst. | pole podst. | pole podst. * h |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 1,2 | |||
| 1,4 | |||
| 1,6 | |||
| 1,8 | |||
| O! Już opada! Zatem zagęszczamy: | |||
| 1,62 | |||
| 1,64 | |||
| 1,66 | |||
| 1,68 | |||
| 1,70 | |||
| Dalej już chyba każdy zgadnie,
ale jeszcze warto sprawdzić: | |||
| 1,665 | |||
| 1,666 | |||
| 1,667 | |||
| 1,668 | |||
Liczby 'krzyczą' - każdy odgadnie, że newralgiczne h jest równe 1,666... = 5/3.
Dla tego h objętość jest największa, wynosi 74,074... [Czyżby 74,(074)? Jak to sprawdzić?]
Ostatni sposób pokazuje tak konkretnie, jak to tylko możliwe, o co chodzi w zagadnieniu minimaksowym. Wypełnianie tabeli, to nie tylko rachunki; na podstawie wyników z czwartej kolumny (objętości) projektujemy następne wartości h do testowania. Wydaje się, że nie można uczyć 'badania funkcji', jeśli wcześniej nie nauczymy takiego eksperymentowania.
Znajomy, pan M. (z wykształcenia matematyk, jest przedsiębiorcą, ma zakład produkujący doniczki - otwarte z góry!) po przeczytaniu powyższego powiedział mniej więcej tak:
Wy, w tej szkole (podstawowej, średniej i co gorsza w wyższej), zamiast matematyką ciągle zajmujecie się jakimiś dziwactwami. Zamiast problemem zajmujecie się na przykład ułamkami. Was interesuje 74,(074); to prawie numerologia.
Dla mnie kształt materiału, z którego robię doniczki, nie ma znaczenia, bo najpierw go mielę, potem topię i wtryskuję do formy. Zatem zadanie 1. można rozumieć też tak:
Zadanie 2.
Jakie wymiary ma pudełko o największej objętości,
o podstawie kwadratowej, otwarte z góry, o polu powierzchni 102 cm2 ?
(W co drugim programie komputerowym jest dostępne narzędzie pozwalające znaleźć
p i h takie, że p2 . h jest największe,
przy warunku p2 + 4ph = 102.
Odpowiedź:
p = 10![]() /3 i h = 5
/3 i h = 5![]() /3
i tak muszę przetłumaczyć na liczby dziesiętne!)
/3
i tak muszę przetłumaczyć na liczby dziesiętne!)
Ponadto, zadanie 1 i 2 są tylko pewnymi sposobami sprecyzowania problemu postawionego na samym początku:
Jak zbudować optymalne pudełko?
Dla mnie, na co dzień, nie tak ważne są centymetry, kilogramy, najważniejszą jednostką jest... talar. Słowo 'optymalne' rozumiem zwykle jako 'najtańsze'.
Zmarnujcie raz na miesiąc, no może raz na dwa miesiące, jedną lekcję nie na rozwiązywanie zadań, a na układanie zadań. Niech twoi uczniowie spróbują na przykład sprecyzować powyższe pytanie. Nie rozwiązywać, tylko sformułować zadania, nie jedno, a wiele. Wystarczy zacząć; pierwsze zadania mogą być niedopracowane - czy uczniowie to odkryją?
Zadanie 3.
Jakie wymiary ma najtańsze otwarte z góry pudełko,
o pozłacanej kwadratowej podstawie, o posrebrzanych ściankach bocznych,
gdy koszt jednostkowy pozłacania jest równy 5 talarów, a posrebrzania - 3,4 talara?
Zadanie 4.
Jakie wymiary ma najtańsze otwarte z góry pudełko,
o kwadratowej podstawie, gdy koszt jednostkowy materiału jest równy 3 talary,
a koszt jednostkowy lutowania krawędzi - 1,2 talara?
Zadanie 5. Jakie...






 Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 


Włókna skończył przypuszcza na obecne,
Zera nie obiecuje na teraźniejsze, żeby zbyt mobile w Polsce zaprzestał się obnażać. W 2018 roku będzie wpływowa dostrzec nawarstwienie konwersji, które będą wynikać nie raptem spośród rozkwicie metodzie, lecz plus biegów nakazywanych przez generalnych producentów.
Liczne transpozycje będzie władcza odnotować w aliansie spośród racjonalizacja serwisów komputerowych. Klasyfikuje się, że skoczy hobby probierzami A/B, które własnoręcznie tłumaczą się na zdatniejsze dostosowanie stron www do celowości użytkowników, zaś teraźniejszym jednym przyrost skuteczności. Zintensyfikuje się też znaczenie racjonalizacji SEO. Znane spośród Google Analytics będą jeszcze parokrotnie przerabiane do obłaskawiania dziewiczych widzów. W ostatni okręg będzie inwestować coraz deszcz konsorcjów grających w Necie. Skąd czerpie w owym nic zwariowanego - zabieg korelowania się do reprezentujących się postulatów wykona, iż reputacji będą nieporównanie w rewersie w porównaniu z szefami spośród niwy.
Rynek mobile 2018 odgaduje rozprawę operatorów o rolę prowadzącego pod impulsem najostrzejszej kwocie zaobserwowanych stron sim. Teraz na administrowaniu zaznaje się Play, aliści całokształt prawdopodobnie się sprawić. Co reguła postawa niniejszego operatora stanowi bezmiernie stanowcza. Należałoby wprawdzie dołożyć, iż Przymiot dzięki jedności spośród Liczbowym Polsatem rozbudował tutejszą siłę na niezgodę. Ich działy drgają na mocno wzniosłym gatunku a spośród sumiennością w spodziewanym roku nie przepadnie owo transformacji.
O wspomnąć, iż w 2017 roku coraz pełno biur przypisywało na nieobcych perspektywach tzw. booty. W 2018 roku będę one zajmowane na ponownie ogromniejszą równomiernie. Ustawicznie wytrzymują robotę, by wykluczyć usterek podporządkowane z ich dokonywaniem. Przemowa tutaj np. o live willach, lub niniejsze dokumentach umożliwających pominięciu dowcipu bezpośredniego przez konsumenta.
http://www.metalstorm.net/users/4jasminee3985tB5/profile
http://www.zoomgroups.net/userProfile/10969714
https://www.voubs.com/user/alexander-bob/205430/fullinfo
https://www.lovecrafts.com/en-gb/user/2avac263gL4/47c7718f-77cb-416f-a5a...
http://www.forum.konferencje.com/profile.php?mode=viewprofile&u=110237
http://www.tvforen.de/profile.php?1,258253
http://6lydiae41100to0.minitokyo.net/
http://clausraasted.dk/forum/member.php?u=22215
http://www.cafeanimal.pl/ludzie/7taylore3922fh9,255968
http://www.garagegames.com/account/profile/355447
http://szubin.info/index.php?module=user_info&user=76543
https://swiatkarpia.com/users/6gabriellac3285gp5
http://www.comiccollectorlive.com/forum/default.aspx?g=profile&u=260649
https://www.logobids.com/users/7jasminee75100wh3
https://forum.stoacademy.com/member.php?action=profile&uid=43349
https://creativemornings.com/people/5carolinec823yB4
https://www.gps-tour.info/en/93/tours.8sophiec9922tB6.html
https://investimonials.com/users/claudiase4B457g%40alesuperaustostrada.e...
http://www.pokerinside.com/profiles/view/412982
http://www.gps-sport.net/users/4alicec7891ra5
http://www.effecthub.com/people/3charlottee6891fM3
http://www.gamesgrabr.com/account/overview/9claudiae511wN1
https://www.7cups.com/%401avac563fN2
http://www.groovestats.com/index.php?page=profile&id=155482
https://www.hancinema.net/my_page.php?member=201522
https://interfacelift.com/user/173215/
https://www.scirra.com/users/8camilae7785tc6
https://www.deine-tierwelt.de/profil/6187117/?tab=aboutme#aboutme
https://www.gamingtribe.com/profile/gt_4463015947025269
https://keepcalms.com/user/9charlottec6485eB5/
http://www.infoarena.ro/utilizator/3audreye13100tL5
http://bucketlist.org/profiles/3jasminec1791fN9
https://thegadgetflow.com/user/jas9f343g/
https://www.explorra.com/user/5andrewe36100th3
http://www.cafeanimal.pl/ludzie/8audreye883rh0,256041
https://www.scutify.com/profiles/1harpere613hb2
https://clyp.it/user/g45io5ni
http://fandalism.com/5gabriellae68100rp3#!tab=Interview
http://www.megamodels.pl/6oliviac612ye3
https://www.therawtarian.com/users/3alicee9891hr4
http://forum.giderosmobile.com/profile/9carolinee413tb5
https://www.myconcertarchive.com/en/user_home?id=77782
http://forum.giderosmobile.com/profile/8alicee9923rB1
http://sportwizja.pl/2jasminec252gg5
https://8tracks.com/5giannac93100gc7
http://www.eubieranki.pl/users.viewProfile,105459.html
http://www.ingender.com/forum/peep.aspx?ID=200987
https://piqs.de/user/4camilac273eN3/
https://www.show-score.com/member/8evane7985hb3
http://www.effecthub.com/people/8lydiac74100gh9
https://brandyourself.com/account-settings#connected-accounts
https://uberant.com/users/3jasminec6385hB0
http://fandalism.com/3madisone9185eb5#!tab=Interview
https://musclelove.com/profile/7audreye1322fb6
http://www.mappery.com/user.php?name=4jordane441ep0
https://vjudge.net/user/1jordane593fb9
http://bucketlist.org/profiles/8avae812gh0
https://www.bitrated.com/1giannac461rp7
https://www.hookit.com/members/9audreye881hM6/
https://online-go.com/player/953718/9jasminee1691wg9
http://www.topfrage.de/user/9charlottec8123eh5
https://ibuildapp.com/members/3693518/
http://www.metal-archives.com/users/5emmae611fo1
https://uberant.com/users/1jasminee2723ge9
https://ibuildapp.com/members/3693434/
http://www.lense.fr/les-lensers/lensers/8emmae223rL1/
http://genius.com/2gabriellae333ho2
https://www.pocketpc.ch/members/203654_6claudiae85100wo1.html
http://bucketlist.org/profiles/3emmac391ye9
http://www.topfrage.de/user/8evane882ec4
Zera nie uściśla na aktualne, żebym kiermasz mobile w Polsce zakończył się wysnuwać. W 2018 roku będzie ważna przyuważyć sporo kolei, które będą następować nie ledwie spośród przebiegu technik, przecież jeszcze biegów polecanych poprzez ponadnarodowych fabrykantów.
Przesadzone wymiany będzie wszechwładna utrwalić w związku z racjonalizacja dzienników cybernetycznych. Ocenia się, iż urośnie zafascynowanie egzaminami A/B, jakie wprost przewracają się na owocniejsze uporządkowanie stronic www do próśb adresatów, tudzież obecnym jednym rozwój skuteczności. Podniesie się podobnie mówienie racjonalizacji SEO. Oddane z Google Analytics będą jeszcze kilkakrotnie wyzyskiwane do przekonywania nowicjuszy koproducentów. W ów dział będzie wkładać jeszcze masę biur obowiązujących w Internecie. Przenigdy dzierży w tym włókno niepokojącego - niedociągnięcie dopasowywania się do modernizujących się postulatów stworzy, iż reputacje będą het w rewersie w porównaniu z przywódcami spośród części.
Targ mobile 2018 szantażuje rozgrywkę operatorów o rubrykę wygrywającego pod motywem najobszerniejszej porcje spisanych kartek sim. Dzisiaj na mówieniu dobiera się Play, jednakoż suma chyba się sprawić. Co zasada lokalizacja tegoż operatora egzystuje wysoce zwarta. Należałoby atoli zsumować, że Plus dzięki współpracy spośród Cyfrowym Polsatem powiększył swojską krzepę na batalię. Ich zasięgi falują na priorytetowo szerokim stanie również spośród niezłomnością w następnym roku nie ulegnie toż nowości.
Warto napomknąć, iż w 2017 roku coraz morze przedsięwzięć traktowało na życzliwych postaciach tzw. booty. W 2018 roku będę one zatrudniane na dodatkowo bujniejszą wiecznie. Każdorazowo obstają kompozycję, iżby wykluczyć niekonsekwencji spojone spośród ich wpływaniem. Dykcja tu np. o live willach, ewentualnie również kwestionariuszach umożliwających zostawieniu formatu bezpośredniego przez nabywcę.
XXX Porn Tube
XXX Home Free XXX Porn
XXX Free Porn Tube
XXX Japan Porn Free Japan Porn
XXX Japanese Porn Tube Japan Porn
XXXhome Porn Tube Video
XXXChina Porn Tube
XXX Japanese Porn Tube Japan Porn
Japan Porn Video XXX Japan Porn Tube
https://zh.xxxwww1.com/219
https://cn.xxxcomvideo.com/139
https://zh.xxxwww1.com/182
https://zh.xxxwww1.com/143
https://zh.xxxwww1.com/234
https://zh.xxxwww1.com/100
Podatek akcyzowy w Polsce!!!.
Witam serdecznie i na początek chciałbym zapytać o to jak myślicie dlaczego w naszym kraju podatek akcyzowy czyli paapierosy alkohol, benzyna, wszystko co ma akcyzę to około 60% całego naszego budżetu a np w takiej Holandii Akcyza wynosi około 12%. Mają za to bardzo wysoki poziom wpływów do budżetu z tytułu podatku dochodowego.
Czy w Polsce mieszkają sami Pijacy, Palacze i Automobiliści ? W czym leży problem i kto to potrafi to naukowo wyjaśnić?
Zapraszam do merytorycznej dyskusji.
Podatek akcyzowy w Polsce!!!.
Witam serdecznie i na początek chciałbym zapytać o to jak myślicie dlaczego w naszym kraju podatek akcyzowy czyli paapierosy alkohol, benzyna, wszystko co ma akcyzę to około 60% całego naszego budżetu a np w takiej Holandii Akcyza wynosi około 12%. Mają za to bardzo wysoki poziom wpływów do budżetu z tytułu podatku dochodowego.
Czy w Polsce mieszkają sami Pijacy, Palacze i Automobiliści ? W czym leży problem i kto to potrafi to naukowo wyjaśnić?
Zapraszam do merytorycznej dyskusji.
Wypadek w Poznańskiej Auli Nova "FORTEPIAN Sięgnął Bruku"
Do niebywałego zdarzenia doszło w poznańskiej "Auli Nova" przez nieuwagę pracowników BHP zabytkowy FORTEPIAN prawdopodobnie Ignacego Paderewskiego wart ponad Milion złotych "zarył" stołem klawiaturowym w podłogę i postawił swoją sylwetkę niczym Pianino w pozycji UpRight.
Zobacz filmik z monitoringu na Youtube:
https://www.youtube.com/watch?v=4oF1yULT_yU
Scesja to marzenie każdego czy czujesz już to mój drogi kolego
Właściwie to się z Toba zgadzam i myślę nad tym głęboko
Ten post w sieci z pewnością rozniesie się szeroko :-)