W trójkąt równoboczny można zapakować trzy jednakowe kwadraty na wiele sposobów. Poniżej widać cztery sposoby pakowania.
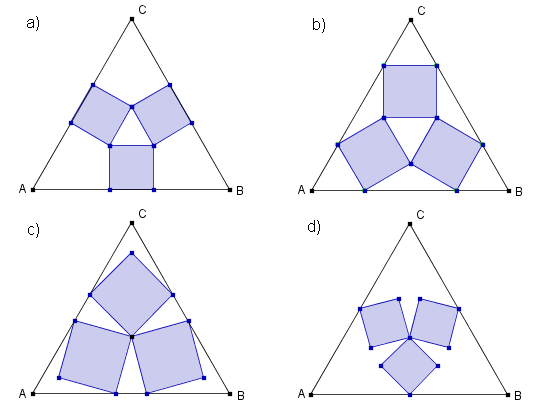
Rozgrzewka. Oblicz długości boków kwadratów, gdy bok trójkąta ma długość a.
Zajmiemy się teraz następującym problemem:
Przypadek a)
Widać, że kwadraty mogą się przesuwać (najpierw wzdłuż boków).
Przypadek d)
Wydaje się, że nie można przesunąć dolnego kwadratu, bo podstawa trójkąta i pozostałe kwadraty blokują go.
Ale można go obrócić. Nie względem środka kwadratu, ale względem punktu O - środka trójkąta.
Przypadek b)
Zobaczmy, że nie można obrócić lewego kwadratu względem punktu K.
Co prawda wierzchołki L i M mają pewną swobodę, ale
- obrót w lewo blokuje bok AC trójkąta,
- obrót w prawo blokuje prawy kwadrat (blokując bok LM).
Sprawdź też, że nie można obracać lewego kwadratu względem jego środka. Co ten obrót blokuje?
Jednak w przypadku b) kwadraty też telepią się, bo mogą się obracać względem punktów
OA , OB , OC (patrz poniżej).
Przy małych obrotach (< 30o) boki trójkąta nie blokują tego ruchu.
Nie ma jednak całkowitej swobody. Kwadraty muszą obracać się w tę samą stronę.
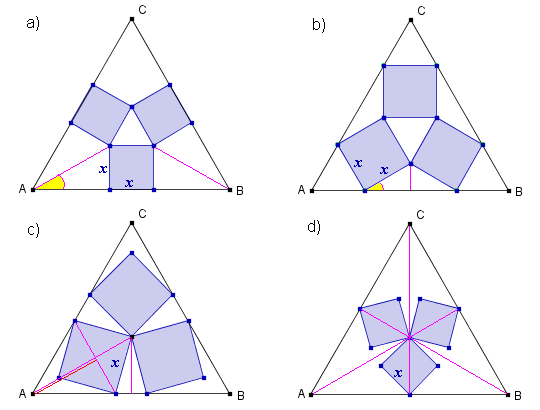
Oblicz odległości: OAL,
OAOB;
sprawdź, że 2OAL > OAOB,
- co to oznacza?
Przypadek c)
Wyznaczmy punkt OA podobnie jak w przypadku b) (patrz poniżej).
Zobacz, że nie można obrócić lewego kwadratu względem punktu OA, bo prawy, górny wierzchołek jest 'uwięziony' przez boki pozostałych kwadratów.
Sprawdź, że lewego kwadratu nie można obrócić względem innych punktów (przesuń O i ruszaj suwakiem).
Jednak i w tym przypadku kwadraty telepią się. Dlaczego? Mogą się obrócić wszystkie naraz. Zobacz. Powiększ rysunek [zoom], by lepiej zobaczyć, jak kwadraty 'rozjeżdżają się' w środku trójkąta.
To jest nieco podobne do jednoczesnego 'rozchodzenia się' kwadratów z przykładu d).
Pojedynczego kwadratu nie można przesunąć, ale można przesunąć wszystkie jednocześnie, w kierunkach wyznaczonych przez boki trójkąta. Zobacz.
PROBLEM *.
Czy jest jakiś sposób zapakowania trzech jednakowych kwadratów w trójkąt równoboczny, w którym kwadraty nie przemieszczają się?
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
