Jak buduje się piramidy?
Sprawdź, bawiąc się poniższym "generatorem piramid".
Sprawdź, jakie wysokości i objętości mają stworzone przez Ciebie
piramidy o zadanej podstawie.
Piramidy:
Umowa. Dalej piramidy będziemy rysowali tylko z 'lotu ptaka', czyli tak, jak wyglądają z góry. Na rysunkach bok kratki ma długość 1. Wszystkie wymiary będziemy podawali w tych właśnie jednostkach.
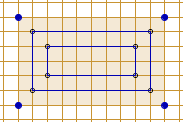Piramida obok ma podstawę prostokątną, na której leży pierwsza warstwa 60 bloków sześciennych.
nad brzegiem poprzedniej jest galeria szeroka na jeden blok.
Złożona jest 6 . 10 + 4 . 8 + 2 . 6 = 104 bloków,
gdy są to bloki 1×1×1, to jej objętość jest równa 104.
Ma wysokość 3, jej pole jest równe 192 (łącznie z polem 'od dołu').
Jej 'cień WE' (przy oświetleniu z zachodu) ma pole 12,
jej 'cień SN' (przy oświetleniu z południa) ma pole 24.
Taką bryłę nazwiemy:
1 - piramidą,
gdy zbudowana jest z bloków 1×1×1,
0,5 - piramidą,
gdy zbudowana jest z bloków 0,5×0,5×0,5,
0,1 - piramidą,
gdy zbudowana jest z bloków 0,1×0,1×0,1.
Jaką wysokość ma 0,5-piramida
o podstawie prostokąta 6×10?
Z ilu bloków się składa? Jaką ma objętość?
Wskazówka: blok 1×1×1 składa się z 8 bloków 0,5×0,5×0,5.
Uwaga.
0,5-piramida o podstawie
6×10 wygląda podobnie do
1-piramidy o podstawie 12×20.
Jaki jest związek między ich wysokościami? Objętościami? Polami?
Wzór. Liczba bloków
1-piramidy o podstawie
prostokąta m × n, równa się
n liczby naturalne.
Ten wzór można wykorzystać do obliczania objętości
0,25-piramid o podstawach prostokątnych. Jak?
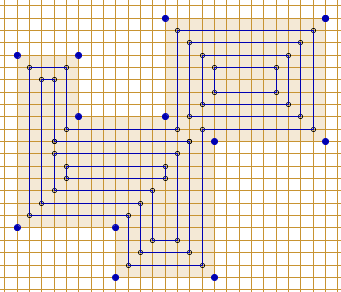
1-piramida obok ma
wysokość 5 przyjmowaną na dwóch "wyżynach".
Sprawdź, że pole pierwszej galerii jest o 4 mniejsze od obwodu podstawy.
Czy to jest ogólna prawidłowość?
Narysuj jej 'cień WE' i cień SN'.
Porównaj z cieniami 0,5-piramidy o tej samej podstawie.
Jaka jest wysokość 0,5-piramidy o tej samej podstawie?
Jaka jest wysokość 0,1-piramidy o tej samej podstawie?
Proponujemy serię zadań (pochodzą z konkursu KOMA).
Zadanie 1.
Uzupełnij. 1-piramida
o podstawie jak na rysunku m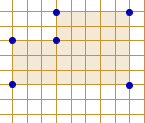a:
a)
wysokość . . . . .
objętość . . . . .
pole . . . . .
pole cienia WE . . . . .
b)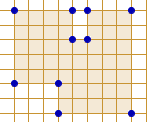 
wysokość . . . . .
objętość . . . . .
pole . . . . .
pole cienia WE . . . . .
Zadanie 2.
Jakie pole ma cień SN 1-piramidy o
podstawie kwadratowej o danych wymiarach?
a) 7×7 b) 14×14 c) 17×17
Zadanie 3.
Jakie pole ma cień SN 0,5-piramidy o
podstawie kwadratowej o danych wymiarach?
a) 7×7 b) 8×8 c) 9×9
Zadanie 4.
Ile jest 1-piramid o podstawie prostokątnej
o danym polu podstawy?
a) 24 b) 124 c) 1024
Zadanie 5.
Jaką najmniejszą objętość może mieć 1-piramida o danej wysokości?
a) 4 b) 5 c) h
Zadanie 6.
Ile jest 1-piramid, których oba cienie SN i WE są jednakowe i takie, jak na rysunku?
a)
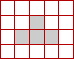b)
c)
Zadanie 7. Uzupełnij zdania:
a)
1-piramida o podstawie kwadratowej
10×10 ma objętość . . . . . . . i pole . . . . . . .
b)
0,5-piramida o podstawie kwadratowej
10×10 ma objętość . . . . . . . i pole . . . . . . .
c)
0,25-piramida o podstawie kwadratowej
10×10 ma objętość . . . . . . . i pole . . . . . . .
Zadanie 8.
Jakie boki podstaw mają dwie 1-piramidy o podstawach kwadratowych, których:
a)
objętości różnią się o 36?
b)
objętości różnią się o 64?
c)
pola powierzchni różnią się o 64?
Dalszy ciąg historii piramid, które przestaną być dyskretne, znajdziesz tutaj.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
