Zadania o podziale figur na mniejsze, przystające części, przy ewentualnym zachowaniu pewnych dodatkowych warunków, często występują wśród łamigłówek matematycznych. Nie wymagają na ogół żadnej specjalistycznej wiedzy, jedynie wyobraźni geometrycznej, spostrzegawczości i odrobiny wprawy. Świetnie nadają się na kółko matematyczna lub zajęcia na zielonej szkole.
Prezentowane niżej zadania pochodzą z różnych edycji Międzynarodowych Mistrzostw w Grach Matematycznych i Logicznych. Ułożone są ze względu na rosnący stopień trudności, co powinno ułatwić ich rozwiązywanie lub wykorzystanie na kółku matematycznym. Większy wybór zadań z tego konkursu można znaleźć na stronie internetowej http://www.gmil.prv.pl.
Prosimy o dopisywanie w komentarzach kolejnych zadań dotyczących podziału figur (ew. rysunki można wysłać e-mailem na adres redaktora działu "Kółko matematyczne"), zamieszczania linków do takich zadań lub dzielenia się swoimi pomysłami rozwiązań.
We wszystkich poniższych zadaniach daną figurę należy podzielić na przystające części, choć czasem zabronione jest odwracanie części podziału na drugą stronę (więc przystawanie realizuje się jedynie przez przesunięcie i obrót). W niektórych przypadkach linie podziału muszą przebiegać wzdłuż zaznaczonych linii, a wierzchołki muszą wypadać w punktach kratowych. Figury uzyskane z podziału zawsze są spójne (tzn. pozostają „w jednym kawałku”) i żadna nie może składać się z części mających tylko jeden punkt wspólny.
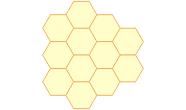
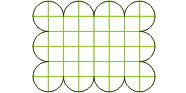
| Zadanie 1. Finał krajowy 1999 Plaster miodu podziel na trzy przystające części, tak aby każda z nich była złożona z całych sześciokątów. Podaj dwa różne rozwiązania. |
|
| Zadanie 2. Finał międzynarodowy 1998
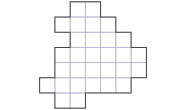
Ojciec Izydor – właściciel parceli – zamierza ją podzielić pomiędzy trzech synów w taki sposób, aby wszystkie części były przystającymi wielokątami złożonymi z całych kratek. Zaznacz ten podział. |
|
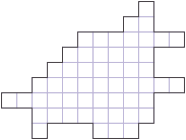
| Zadanie 3. Finał krajowy 2001 Ojciec Izydor podzielił teren na pięć działek mających kształt przystających wielokątów złożonych z całych kratek. Zaznacz ten podział. |
|
| Zadanie 4. Finał międzynarodowy 1999 Stary Szulej, zwany Figowcem, posiadał działkę obsadzoną drzewami figowymi (na rysunku drzewa zaznaczono kropkami). Po jego śmierci trzeba było podzielić ten teren między sześcioro dzieci. Zadanie nie było łatwe, bo każde zażądało parceli tego samego kształtu co pozostałe oraz posiadającej drzewo figowe. Pomóż notariuszowi dokonać podziału. |
|
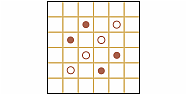
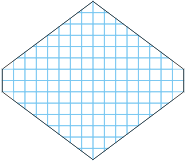
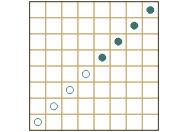
| Zadanie 5. Finał międzynarodowy 1996 Posiadłość magnata Gorliwca ma kształt kwadratu podzielonego na 25 jednakowych sektorów. Rośnie tam pięć wspaniałych cedrów libańskich, na planie zaznaczonych kropkami. Magnat ma cztery córki i pragnie podzielić między nie swoją posiadłość, zostawiając jedną parcelę sobie. Wszystkie działki mają mieć jednakową powierzchnię oraz:
Jak dokonać podziału spełniającego powyższe warunki? |
|
| Zadanie 6. Lista treningowa – Bobowicko 1997
Kwadratową działkę podziel na cztery części jednakowego kształtu i wielkości tak aby:
|
|
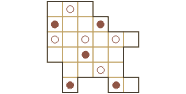
| Zadanie 7. Półfinał krajowy 2002 Na działce starego Tomasza rośnie 5 jabłoni i 5 grusz. Podzielił on ten teren między swoich pięciu synów. Każdy z nich otrzymał parcelę w kształcie przystającego wielokąta z jedną gruszą i jedną jabłonią (które nie muszą wypadać w tym samym miejscu). Zaznacz podział na rysunku. |
|
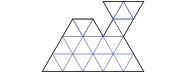
| Zadanie 8. Finał krajowy 2004 Figurę z rysunku podziel na trzy przystające wielokąty dające się nałożyć jedynie przez przesuwanie i obracanie. |
|
| Zadanie 9. Półfinał krajowy 2001 Magda zaprosiła na imieniny dwie przyjaciółki, które przyniosły w prezencie nietypowy placek z polewą miodową. Jak podzielić go na trzy części tego samego kształtu i takiej samej powierzchni? Ze względu na polewę, części te nie mogą być odwracane. |
|
| Zadanie 10. Eliminacje 1999 Figurę z rysunku podziel na sześć przystających części. |
|
| Zadanie 11. Finał międzynarodowy 1998 Walenty otrzymał na urodziny duży piernik. Na przyjęcie zaprosił pięciu przyjaciół i po namyśle udało mu się podzielić piernik na sześć porcji o jednakowej powierzchni i kształcie. Jak to zrobił? |
|
| Zadanie 12. Finał krajowy 1997 Plac pokazany na rysunku podziel na cztery przystające parcele. |
|
| Zadanie 13. Finał krajowy 1995 Podziel figurę z rysunku na cztery przystające części. |
|
| Zadanie 14. Finał międzynarodowy 1995 Na rysunku przedstawiono obszaru jednego z województw. Podziel go na 8 powiatów w kształcie przystających wielokątów. |
|
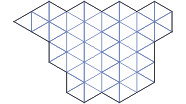
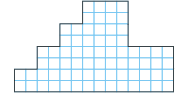
| Zadanie 15. Finał międzynarodowy 2005 Podium olimpijskie widziane z boku ma kształt przedstawiony na rysunku. Czy potrafisz rozciąć je według linii kratkowania na trzy kawałki w taki sposób, aby otrzymać dwie przystające figury oraz trzecią, która jest figurą podobną do tamtych dwóch? |
|
| Zadanie 16. Tnij waść Jak rozciąć figurę z rysunku na dwie przystające części? |
|
| Zadanie 17. Ying-Yang na dwa Działka z rysunku ma kształt wzorowany na symbolach Yin-Yang. Podziel ją na dwie przystające części. |
|
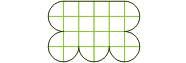
| Zadanie 18. Ying-Yang na trzy Podziel działkę z rysunku na trzy przystające części. |
|
| Zadanie 19. Działka do podziału Rysunek przedstawia działkę, na której rosną 4 dęby i 4 klony. Podziel ją na 4 przystające części, tak aby na każdej rósł 1 dąb i 1 klon. |
|
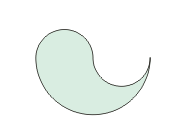
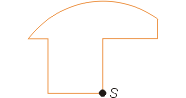
| Zadanie 20. Krzywoliniowa działka Krzywoliniowy brzeg działki przedstawionej na rysunku, to ćwierć okręgu o środku w punkcie S. Podziel tę działkę na dwie przystające części. |
|
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
