| więcej informacji o tekście: |
Nie będziemy się zajmować puszkami, które stoją w koszu.
Mają one:
- osie równoległe do osi kosza,
- podstawy równoległe do podstawy kosza,
- osie prostopadłe do podstawy kosza,
- podstawy prostopadłe do osi kosza
i... nie są ciekawe.
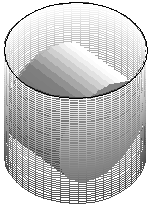
Zbadamy puszki, które leżą w koszu, to znaczy puszki, które mają:
- osie prostopadłe do osi kosza,
- podstawy prostopadłe do podstawy kosza,
- osie równoległe do podstawy kosza,
- podstawy równoległe do osi kosza
i... są znacznie ciekawsze.
Poniżej widać kilka takich puszek.
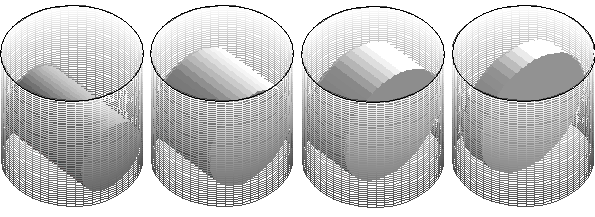
 Mają one wspólną cechę, której nie widać na powyższym rysunku.
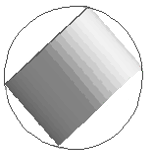
Byłoby ją (tzn. tę cechę) widać, gdyby patrzeć z góry, tak jak na
rysunku po prawej.
Te puszki nie 'telepią się', gdy poruszyć koszem, nie brzęczą, nie przemieszczają się, leżą ciasno dopasowane do kosza. Jak sprecyzować tę własność?
Mają one wspólną cechę, której nie widać na powyższym rysunku.
Byłoby ją (tzn. tę cechę) widać, gdyby patrzeć z góry, tak jak na
rysunku po prawej.
Te puszki nie 'telepią się', gdy poruszyć koszem, nie brzęczą, nie przemieszczają się, leżą ciasno dopasowane do kosza. Jak sprecyzować tę własność?
Można tak:
gdy H oznacza wysokość kosza i R - promień podstawy kosza,
a h oznacza wysokość puszki i r - promień podstawy puszki, to
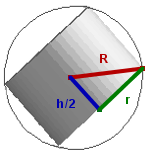 R 2 = r 2 + (h/2) 2 .
R 2 = r 2 + (h/2) 2 .
Wśród takich puszek jedna ma największą objętość. Zbadajmy która, tzn. obliczmy jej wymiary w zależności od R.
Mianowicie:
V = ![]() r2 h
=
r2 h
= ![]() . (R 2 - (h/2) 2) . h
=
. (R 2 - (h/2) 2) . h
= ![]() R 2 . h
-
R 2 . h
- ![]() / 4 . h 3,
/ 4 . h 3,
V ' =
![]() R 2
- 3/4
R 2
- 3/4 ![]() . h 2,
. h 2,
V ' = 0
dla
h = 2![]() /3 . R .
/3 . R .
Zatem puszka o największej objętości umieszczona w koszu ma wymiary:
wysokość = 2![]() /3 . R
i promień podstawy =
/3 . R
i promień podstawy = 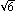 /3 . R .
/3 . R .
Nie jest to całkiem poprawne rozwiązanie, bo... czasami takie puszki wystają, nie mieszczą się w koszu.
Zadanie 1. Przy jakiej wartości H taka puszka nie wystaje z kosza?
Zadanie 2. Jaki jest największy stosunek objętości puszki do objętości kosza, dla puszek całkowicie zawartych w koszu?




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
