| więcej informacji o tekście: |
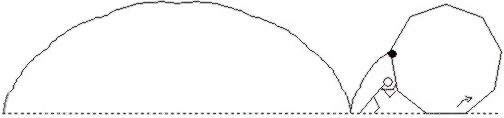
Toczymy po prostej n-kąt foremny. Zbadajmy, jaką trajektorię kreśli ustalony wierzchołek.
Trajektorie są przybliżane przez niebieskie łamane; przyjrzyjmy się im dokładniej:
Popatrzmy.



Pole pod tą łamaną dla n = 3, 4, 6 jest trzykrotnie większe niż pole
toczącego się wielokąta.
Czy tak jest zawsze?
HIPOTEZA. Dla każdego n-kąta foremnego

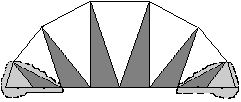
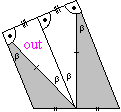
Poszukamy ogólnego rozumowania (rysunki są dla n=8). Przyjmijmy oznaczenia jak poniżej:
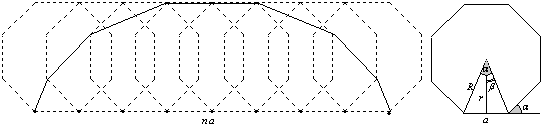
Zauważmy, że zaznaczone odcinki i kąty
 są równe
są równe
i to
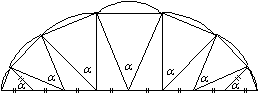
 się składa do
się składa do
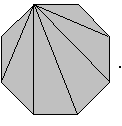
(Dlaczego wychodzi n-kąt foremny?).
Ponadto:
ponieważ
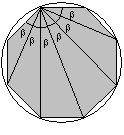 ,
więc czworokąt
,
więc czworokąt
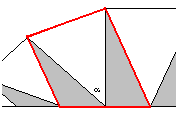
jest trapezem
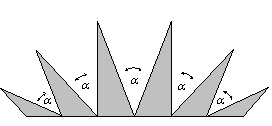
 i pole białego trójkąta jest sumą pól jego szarych 'sąsiadów'.
i pole białego trójkąta jest sumą pól jego szarych 'sąsiadów'.
|
Aby zsumować pola białych klinów, wystarczy więc obliczyć podwojoną sumę szarych trójkątów (również tych skrajnych, patrz rys.).
Zatem
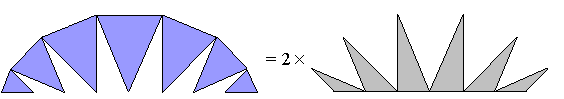
i mamy
TWIERDZENIE. Dla każdego n-kąta foremnego
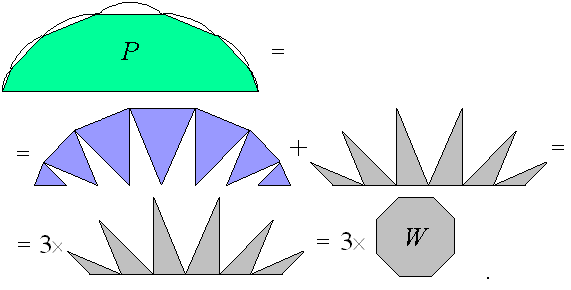
WNIOSEK.
Gdy będziemy toczyć koło o promieniu r
,

to

Teraz znajdziemy długość L łamanej
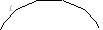 ,
tzn. długość przybliżenia trajektorii wierzchołka toczącego się
n-kąta foremnego po wykonaniu jednego obrotu.
,
tzn. długość przybliżenia trajektorii wierzchołka toczącego się
n-kąta foremnego po wykonaniu jednego obrotu.
|
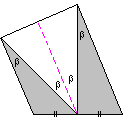
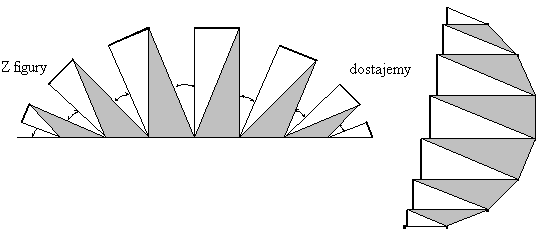
W trapezach widzimy, że jedno z ramion jest prostopadłe do podstaw.
Wycinamy połówki białych trójkątów równoramiennych
i resztę składamy, obracając (n-1) razy o kąt $\beta$ .
|
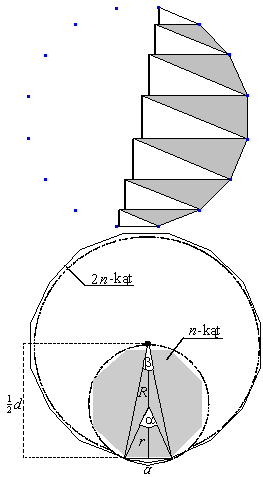
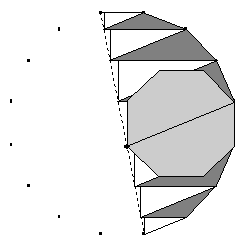
To wygląda na część 2n-kąta foremnego. (Lepiej to widać po zaznaczeniu wierzchołków.)
Sprawdź, że:
- jest to część 2n-kąta foremnego (porównaj kąty i boki),
- boki tego 2n-kąta foremnego mają długość a,
- odcinki wyglądające na poziome, są równoległe (porównaj odpowiednie kąty),
- odcinki wyglądające na pionowe, są równoległe (bo są prostopadłe do tych poprzednich).
Łączna długość pionowych odcinków jest połową szukanej wielkości L (dlaczego?) i jest równa średnicy okręgu wpisanego w ów 2n-kąt foremny (dlaczego?).
Rysunek obok pokazuje, że promień okręgu wpisanego w ów 2n-kąt foremny jest równy sumie promieni okręgów wpisanych i opisanych na oryginalnym n-kącie foremnym. Zatem mamy
TWIERDZENIE L = 4 (R + r) .
Zamiast n-kąta weźmy okrąg o promieniu r toczący się po prostej. Ustalony punkt okręgu wykreśla linię zwaną cykloidą.
TWIERDZENIE
Dla cykloidy:

mamy

oraz

UWAGA
|
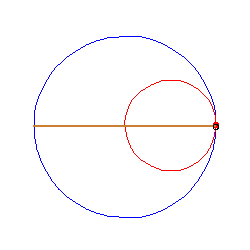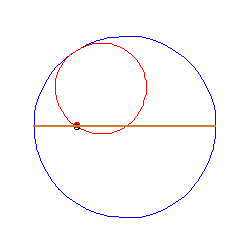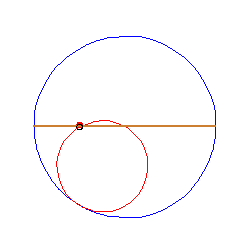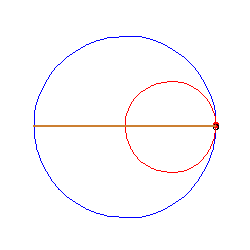
TWIERDZENIE KOPERNIKA
Gdy wewnątrz okręgu toczy się (bez poślizgu) okrąg styczny o połowę mniejszym promieniu, to jego punkty poruszają się po średnicach dużego okręgu.

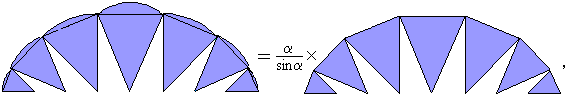 więc
więc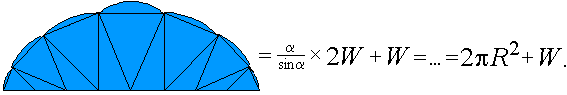
 ,
,



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
