| więcej informacji o tekście: |
|
Rysunki dynamiczne 3D utworzono apletem z www.javaview.de/.
Można nimi manipulować, trzymając lewy przycisk myszy. Jeśli po kilkunastu sekundach rysunki nie wyświetlają się, kliknij . |
Gdy badaliśmy rozety opisane na wielokątach cyklicznych (tzn. takich, na których można opisać okrąg), okazało się, że ich obwody i pola wyrażają się dość prostymi wzorami (patrz artykuł Rozety: wpisana w wielokąt i opisana na wielokącie). Co więcej, uzasadnienia tych wzorów były łatwe i czysto geometryczne. Tu zbadamy analogiczne rozety dla wielościanów.
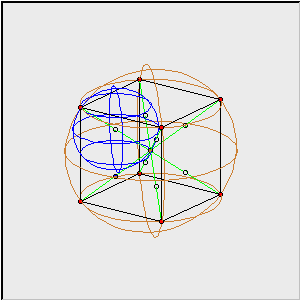
Gdy na wielościanie można opisać kulę, to można też opisać na nim rozetę utworzoną w następujący sposób:
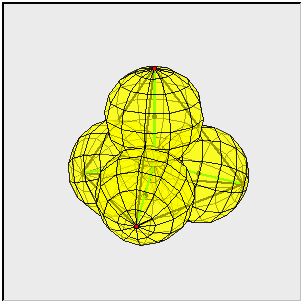
Rozeta opisana na sześcianie
Wyznaczymy Pr - pole powierzchni rozety opisanej na sześcianie o krawędzi a.
Promień Ro kuli opisanej na sześcianie ma długość taką, jak połowa przekątnej, Ro = ![]() /2 a.
/2 a.
Jej środek O jest punktem przecięcia przekątnych sześcianu.
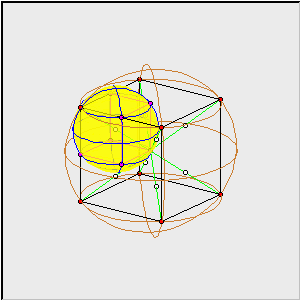
Rozeta opisana na sześcianie składa się z ośmiu kul o promieniach
Rr = Ro/2 =
![]() /4 a.
/4 a.
Kule te nachodzą na siebie (nie są rozłączne).
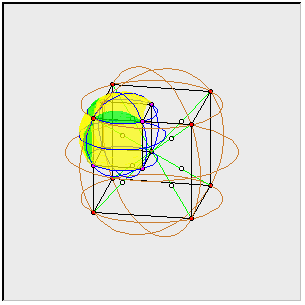
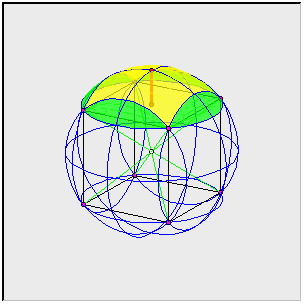
Na powyższym rysunku słabo widać szczegóły. Niemal cały sześcian schowany jest we wnętrzu rozety. Zatem popatrzmy tylko na jedną z ośmiu kul i to 'obdartą ze skórki'.
Zatem każda z ośmiu kul tworzących rozetę jest opisana na sześcianie (różowym) o krawędzi a/2.
Przy czym tylko część ich powierzchni tworzy powierzchnię rozety.
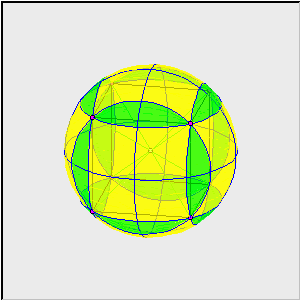
Mianowicie gdy pomyślimy o płaszczyznach ścian tych małych sześcianów (o krawędzi a/2), to podzielą one powierzchnie mniejszych kul na części żółte i zielone.
Cała powierzchnia rozety składa się więc z nienachodzących na siebie nawzajem części:
z żółtych i z części zielonych. Zatem:
Teraz wystarczy już tylko wyznaczyć te wielkości. Pżół, Pziel.
W tym celu zauważmy, że
Ponadto część żółta i cztery części zielone tworzą czaszę o wysokości h = Rr - a/4.
1 . Pżół + 4 . Pziel = 2
Zatem pole powierzchni rozety jest równe
Zadanie 1.
Wyznacz Vr - objętość rozety opisanej na sześcianie o krawędzi a.
Zadanie 2.
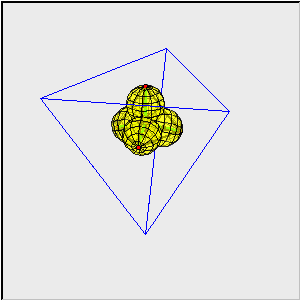
Wyznacz pole powierzchni i objętość rozety opisanej na czworościanie foremnym o krawędzi a.
Zadanie 3.
Wyznacz pole powierzchni i objętość rozety wpisanej w czworościan foremny o krawędzi b.
Zadanie 4.
Wyznacz pole powierzchni i objętość rozety wpisanej w ośmiościan foremny o krawędzi b.





 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
