Różnicą symetryczną zbiorów A i B nazywamy zbiór tych elementów tych zbiorów, które należą do dokładnie jednego z nich. Różnicę symetryczną zbiorów A i B oznaczamy:
B.
Przykłady:
{1, 3, 4, 6, 7, 9}
{3, 5, 6, 7, 8, 9} =
{1, 4, 5, 8}
,
{1, 2, 3, 4, 5, 6}
{4, 5, 6, 7, 8, 9} =
{1, 2, 3, 7, 8, 9}
,
{3, 1, 4, 2, 5, 9}
{1, 2, 9, 8, 5, 6} =
{3, 4, 6, 8}
,
{1, 3, 5, 7, 9}
{2, 4, 6, 8} =
{1, 2, 3, 4, 5, 6, 7, 8, 9}
,
{1, 2, 3, 5, 7, 8, 9}
{1, 2, 3, 5, 7} =
{8, 9}
,
{1, 2, 3, 5, 7}
{1, 2, 3, 5, 7} =
(nic = zbiór pusty) .
Poniższe zadania pozwolą zapoznać się z tym pojęciem.
Niektóre są dość trudne (pochodzą z konkursu KOMA dla uczniów szkół podstawowych).
(Wersja pdf tych zadań jest dostępna tutaj.)
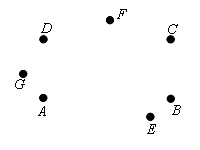
Zad. 1.
Niech P oznacza (pełny) prostokąt ABCD i niech
T oznacza (pełny) trójkąt EFG. Na rysunku zacieniuj
P
T.
Zad. 2.
Uzupełnij:
{1, 3, 4, 6, 7}
{2, 3, 5, 6, 7, 8} = .................................. ,
{1, 2, 5, 7}
{3, 4, 7}
{2, 5, 6, 7, 8} = ........................ ,
{2, 3, 6, 7}
{....................................} = {1, 3, 5, 7, 8, 9} ,
{....................................}
{1, 3, 4, 5, 8} = {1, 2, 3, 7, 8, 9} ,
{1, 3, 5, 7}
{....................................}
{2, 3, 7, 8} = {1, 3, 4, 7, 8} .
Zad. 3.
Podaj takie x, y, że {1, 3, x, y}
{3, 7} = {1, 4} .
Zad. 4.
a)
Podaj taką parę P, R zbiorów czteroelementowych,
o elementach wybranych
spośród liczb 1, 2, 3, 4, 5, 6, że
R = {2, 3, 4, 5} .
b) Ile jest wszystkich takich par P, R spełniających te same warunki?
c) Ile jest wszystkich takich par S, T zbiorów czteroelementowych, o elementach wybranych
spośród liczb 1, 2, 3, 4, 5, 6, że
T = {2, 3, 4} ?
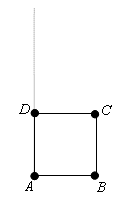Zad. 5.
Niech K oznacza kwadrat ABCD o boku 4
i niech T oznacza trójkąt ABE, gdzie punkt
E leży na półprostej AD.
Oblicz pole figury K
T gdy:
a)
odległość AE jest równa 2,
b)
odległość AE jest równa 4,
c)
odległość AE jest równa 8.
Czy jest takie E na półprostej AD, że
pole K T jest mniejsze od 8?
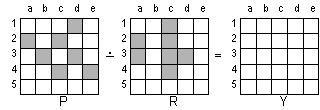Zad. 6.a)
Dla figur:
R = (a2; a3; c1; c2; c3; c4; d3)
R = Y .
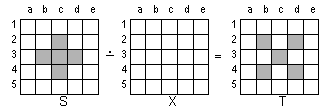Zad. 6.b)
Dla figur:
T = (b2; b4; c3; d2; d4)
Y = T .
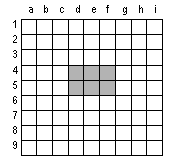
Zad. 7.
Niech S = (d4; d5; e4; e5; f4; f5) czyli S jest pewnym prostokątem kratowym ‘pionowo-poziomym’.
Podaj trzy przykłady takich prostokątów kratowych ‘pionowo-poziomych’ P, że
P jest kwadratem kratowym ‘pionowo-poziomym’.
Zad. 8.
Niech S = (d4; d5; e4; e5; f4; f5) będzie prostokątem
Ile jest takich prostokątów kratowych pionowo-poziomych P, że
P jest figurą o polu 5 (tzn. jest złożoną z pięciu kratek)
a) prostokąt P ma pole 1 (1 kratkę)?
b) prostokąt P ma pole 2 (2 kratki)?
c) prostokąt P ma pole 3 (3 kratki)?
d) prostokąt P ma pole 4 (4 kratki)?
e) prostokąt P ma pole 5 (5 kratek)?
Zad. 9.
Niech A = {2, 3, 4} i B = {3, 4, 5, 6, 7, 8, 9}.
a)
Podaj przykład takiego zbioru C, że
C)
+
liczba el.(C B)
=
liczba el.(A B) .
b) Ile jest wszystkich takich zbiorów C spełniających warunek (*) ?
c) Ile jest wszystkich takich zbiorów E takich, że
E)
=
liczba el.(E B)
=
1/2 .
liczba el.(A B) ?
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
