| więcej informacji o tekście: |
Zbadaj płaskie serca przedstawione na rysunkach.Są przy nich ukryte podpowiedzi - w razie potrzeby naciśnij P. Do zadań bez gwiazdek w zasadzie wystarcza jedynie znajomość twierdzenia Pitagorasa.
Przyjmujemy, że kratki mają wymiary 1 × 1.
 Brzegi serc typu S są zbudowane tylko z ćwiartek okręgów.
Brzegi serc typu S są zbudowane tylko z ćwiartek okręgów.
Zadanie 1. Uzupełnij:
a)
obwód S0 = . . . . . . ,
b)
pole S0 = . . . . . . .
Zadanie 2. Uzupełnij:
|
obwód S1 = . . . . . .
pole S1 = . . . . . . |
obwód S2 = . . . . . .
pole S2 = . . . . . . |
obwód S3 = . . . . . .
pole S3 = . . . . . . |

Zadanie 3. (bez rysunku)
Łatwo sobie wyobrazić figury Sx , dla x pomiędzy 0 i 4.
a)
Czy
obwód Sa + b =
obwód Sa +
obwód Sb ?
b)
Czy
pole Sa + b =
pole Sa +
pole Sb ?
c)
Czy
obwód S 2 . c =
2 . obwód Sc ?
d)
Czy
pole S 2 . c =
2 . pole Sc ?
e)
Czy
obwód S (a+b)/2 =
(obwód Sa + obwód Sb ) / 2 ?
f)
Czy
pole S (a+b)/2 =
(pole Sa + pole Sb ) / 2 ?
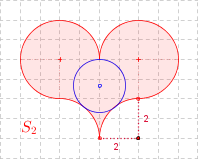
Zadanie 4.
Na rysunku widać największy okrąg zawarty w
S2, o środku leżącym na osi symetri tej figury.
a) Oblicz promień r2 tego okręgu.
b) Oblicz promień r3 takiego okręgu
zawartego w S3.
c) Oblicz promień r1 takiego okręgu
zawartego w S1.
d) W jakiej figurze Sx taki okrąg
ma promień rx = 1 ?
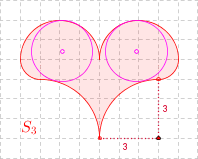
Zadanie 5. Na rysunku widać największy okrąg zawarty w S3. Oblicz jego promień.
Zadanie 6.
Wyznacz promień największego okręgu zawartego w
Sx , dla x pomiędzy 0 i 4.
|
Rysunek utworzony w Geogebrze |
Wskazówka.
Na dynamicznym rysunku obok (kliknij
 )
widać wszystkie okręgi zawarte w Sx, które mają co najmniej dwa
punkty wspólne z brzegiem Sx.
)
widać wszystkie okręgi zawarte w Sx, które mają co najmniej dwa
punkty wspólne z brzegiem Sx.
Można zmieniać x przesuwając (w poziomie) zaznaczony punkt.
Serca typu H wyglądają na prostsze, są ograniczone dwoma łukami okręgów i dwoma odcinkami.

Jednak tak tylko się wydaje. By rozwiązać poniższe zadanie, gdy nie znasz trygonometrii, musisz skorzystać z informacji podanych we wskazówce.
|
obwód H3 = . . . . . .
pole H3 = . . . . . . |
obwód H4 = . . . . . .
pole H4 = . . . . . . |
obwód H5 = . . . . . .
pole H5 = . . . . . . |
|
obwód H6 = . . . . . .
pole H6 = . . . . . . |
obwód H7 = . . . . . .
pole H7 = . . . . . . |
obwód H8 = . . . . . .
pole H8 = . . . . . . |
|
Rysunek utworzony w Geogebrze |
Uwaga.
Na dynamicznym rysunku obok (można przesuwać w pionie punkt K ) widać zależność pomiędzy długością odcinka h w figurze Hh, a miarą kąta
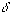 .
.
Można przyjąć, że wielkość h determinuje ową figurę. Również kąt
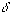 ją opisuje jednoznacznie.
ją opisuje jednoznacznie.
To ostatnie stwierdzenie zanotujemy kodując ową figurę symbolem: H
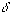 .
.
Zadanie 8. Uzupełnij podając wzór na obwód i pole figury H
 :
:
a)
obwód H 60 = . . . . . .
pole H 60 = . . . . . .
b*)
obwód H 67 = . . . . . .
pole H 67 = . . . . . .
Zadanie 9.
Na rysunku widać największy okrąg zawarty w figurze typu H,
o środku leżącym na osi symetri tej figury.
a) Oblicz promień r60 takiego okręgu
zawartego w H 60.
b*) Oblicz promień r67 takiego okręgu
zawartego w H 67.
c) Oblicz promień r3 takiego okręgu
zawartego w H3.
d)
W jakiej figurze Hh taki okrąg ma promień rh = 2 ?
|
Rysunek utworzony w Geogebrze |
Wskazówka.
Na dynamicznym rysunku obok (kliknij
 )
widać wszystkie okręgi zawarte w danej figurze typu H,
o co najmniej dwóch punktach wspólnych z nią.
)
widać wszystkie okręgi zawarte w danej figurze typu H,
o co najmniej dwóch punktach wspólnych z nią.
Zakończymy trudniejszymi zadaniami (ostatniego nie umiem rozwiązać).
Zadanie 10.
a) Wyznacz funkcję: f ( ) taką, że
H f (
) taką, że
H f (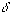 )
= H
)
= H 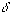 .
.
b*) Wyznacz funkcję g (h ) taką, że
H g (h)
= H h .
c) Wyznacz wzór na długość R (h)
promienia największego okręgu zawartego w Hh.
d*) Wyznacz wzór na długość R' (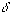 )
promienia największego okręgu zawartego w H
)
promienia największego okręgu zawartego w H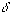 .
.
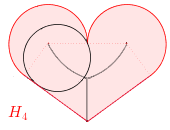
Zadanie 11*.
Środki okręgów zawartych w H4,
które mają co najmniej dwa punkty wspólne z brzegiem H4,
leżą na pewnych liniach. Na jakich?
A jak to jest dla H14 ?
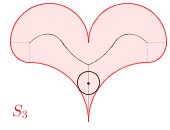
Zadanie 12*.
Środki okręgów zawartych w S3,
które mają co najmniej dwa punkty wspólne z brzegiem S3,
leżą na pewnych liniach. Na jakich?
A jak to jest dla S1 ?
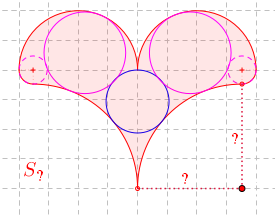
Zadanie 13**.
Na rysunku obok duże różowe okręgi są największymi okręgami zawartymi w figurze typu S.
Wydaje się, że na rysunku obok wszyskie koła są styczne. Czy faktycznie tak jest?
To znaczy, czy istnieje x takie, że w figurze
S x styczne są okręgi przedstawione na rysunku?
Podobne zadania znajdziesz w tekście Serca i łuki (2) .





 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
