| więcej informacji o tekście: |
Wędrówki po siedmiokącie foremnym
A gdzie tu komiwojażer?
Nazwa 'problem komiwojażera' dotyczy zagadnienia znalezienia najkrótszej drogi (lub cyklu) wiodących przez zadane punkty (niekoniecznie przez punkty płaszczyzny). Jak widać, w powyższych kilku szczególnych sytuacjach udało się wskazać najkrótsze drogi i cykle.
Jednak w pełnej ogólności to zagadnienie wygląda na 'beznadziejne' - nie jest dotychczas znany efektywny algorytm wyznaczania takich dróg (efektywny, to mniej więcej znaczy tyle, co oszczędny, czyli taki, by jego działanie nie sprowadzało się do analizowania wszystkich n! możliwych dróg). Co więcej, są podejrzenia, że nie ma takiego algorytmu i nigdy nie będzie.
Może wydawać się że algorytm
Gdyby jednak istniał całkiem ogólny i szybki algorytm znajdowania najkrótszej drogi i najkrótszego cyklu, to niemal ten sam algorytm dawałby rozwiązanie zagadnienia szukania najdłuższej drogi i najdłuższego cyklu. Wynika to z następującej obserwacji.
Obserwacja 11
Ustalmy pewnien 'świat punktów' (Ai, di,j), tj. skończoną kolekcję punktów i odległości pomiędzy nimi (di,j oznacza odległość punktów Ai, Aj).
Niech M oznacza liczbę radykalnie większą od wszystkich liczb di,j (np. M = 4max{di,j} ).
Rozważmy 'nowy świat punktów' (Ai, ei,j)
złożony z tych samych punktów jednak z nowymi odległościami. Niech nową odległością różnych punktów Ai, Aj będzie liczba e i, j = M - di,j.
Wtedy najdłuższa droga w 'świecie' (Ai, di,j) jest najkrótszą drogą w 'świecie' (Ai, ei,j).
To samo dotyczy cykli.
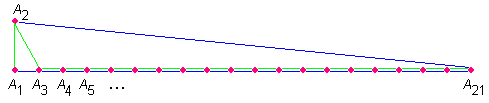
Zilustrujemy, jak wyobrażać sobie 'nowy świat' punktów, na przykładzie, w którym 'stary świat', to 10 punktów na prostej.
Niech M = 4.d1,10 = 4.A1A10.
Wyobraźmy sobie (bo trudno to narysować), że odcinek A1A10 jest grzbietem zeszytu, a na poszczególnych kartkach tego zeszytu narysowane są prostokąty. Kartek jest tyle, co różnych par punktów (czyli 45). Na kartce odpowiadającej parze A3A8 narysowany jest
prostokąt o jednym z boków A3A8 i o obwodzie równym M. Na pozostałych kartkach jest analogicznie.
Teraz trzeba 'zapominać'. Zapomnijmy więc o wnętrzach prostokątów i o wszystkich odcinkach AiAj.
Pozostaną tylko punkty A1, A2,...,A10 i części obwodów prostokątów.
Właściwie 'nowy świat' jest już gotowy. Zobaczmy to na przykładzie. Od A3 do A8 można dojść po pozostałych, nieusuniętych odcinkach. Długość najkrótszej takiej trasy od A3 do A8 reprezentuje nową odległość tych punktów, liczbę e3,8.
Na koniec dodajmy: gdy nie jest znane rozwiązanie optymalne,
trzeba zadowolić się rozwiązaniami 'w miarę dobrymi'. Matematyka próbuje dawać jakieś rozwiązania, o których wiadomo, że są 'w przybliżeniu dobre'. W takim sensie można odczytać rezultat sformułowany w Obserwacjach 10c) i 10e). Nie wiadomo, czy wskazane tam cykle są najdłuższe, ale jeśli nie są, to ich długości różnią się niewiele od optymalnych.
A może ktoś z Państwa znajdzie optymalne rozwiązanie?




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
