Określenie.
Dla zbiorów A, B niech SA,B oznacza
zbiór środków wszystkich odcinków o końcach w A i B.
Będziemy mówili, że SA,B jest środkiem zbiorów A, B.
Przykład. Gdy A, B są skończonymi zbiorami złożonymi z liczb, czyli gdy są podzbiorami osi liczbowej, nietrudno wskazać środek SA,B. Biorąc jedną liczbę z A, a drugą z B, łatwo znajdujemy liczbę leżącą dokładnie po środku między nimi. Powtarzając to dla każdej pary liczb z A i B, otrzymujemy szukany zbiór. Można jeszcze jego elementy uporządkować i wziąć po jednej z liczb występujących w nim wielokrotnie.
Dla A = {1, 2} i B = {1/2, -2, 5, 6} mamy
Dla A = { 1, 3, 1/2} i B = { 1/2, -2, 5, 6} mamy
Tego typu zadania nie są trudne. Są co najwyżej żmudne.
Jest znacznie ciekawiej, gdy A, B są zbiorami złożonymi z punktów płaszczyzny (czyli gdy są figurami płaskimi) lub gdy są zbiorami złożonymi z punktów przestrzeni.
Przykład. Gdy
A = A1A2A3A4
i B = B1B2B3B4B5
są wielokątami wypukłymi, to
SA,B też jest wielokątem wypukłym. Można go zobaczyć następująco:
- środki odcinków o jednym końcu A1 i drugim końcu w dowolnym punkcie B utworzą pomniejszoną (w skali 1/2) kopię B (czyli zbiór SA1,B),
- dla pozostałych wierzchołków A2, A3, A4 jest podobnie,
- szukany zbiór SA,B jest 'rozpięty' na tych czterech figurach:
SA1,B, SA2,B
SA3,B, SA4,B.
Można też postępować odwrotnie: ustalać wierzchołki wielokąta B i patrzeć na zmniejszone kopie A.
Zobaczysz to na poniższym dynamicznym rysunku.
Rysunek dynamiczny utworzony za pomocą GeoGebry.
Przykład. Gdy
A = A1A2A3A4
i B = B1B2B3B4B5
są zamkniętymi łamanymi, to SA,B nie musi być łamaną. Trzeba pracować podobnie, ale 'ostrożniej'.
Ilustruje to poniższy dynamiczny rysunek. Można zacząć od prostszych przykładów, jedną z tych łamanych zamieniając na odcinek.
Rysunek dynamiczny utworzony za pomocą GeoGebry.
Przykład. Gdy
A jest łamaną, a B jest półokręgiem,
SA,B wypełnia pewien obszar płaszczyzny.
Przesuwając punkt P łamanej A, zobaczysz zmniejszona kopię B, czyli środki odcinków o jednym końcu w P, a drugim na całym półokręgu B. Wszystkie takie kopie tworzą szukany zbiór SA,B (kliknij na strzałkę z lewego dolnego rogu rysunku).
Rysunek dynamiczny utworzony za pomocą GeoGebry.
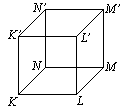Przykład. Gdy
A jest ścianą KLMN i B jest ścianą KNN'K' sześcinu o krawędzi 8 cm, to SA,B jest prostopadłościanem o wymiarach
Poniższe zadania pochodzą z konkursu KOMA'2012.
- Uczniowie szkół podstawowych rozwiązywali zadania bez *.
- Uczniowie gimnazjów zmierzyli się ponadto z zadaniami z *.
- Uczniowie szkół ponadgimnazjalnych mieli jeszcze jedno dodatkowe trudne zadanie 5f**.
Spróbuj i Ty.
Odpowiedzi zobaczysz, klikając w odpowiednie pola lub rysunki.
1. Wypisz elementy zbioru SA,B i podaj, ile elementów ma ten zbiór, gdy:
a)
A = {1, 2, 4}, B = {-2, 0, 4} ,
SA,B =
,
liczba elementów SA,B =
b)
A = { 1/2, 2/3, 1},
B = {2, 4} ,
SA,B =
,
liczba elementów SA,B =
c)
A = {2, 3},
B = { -1, 0, 1, 2} ,
SA,B =
,
liczba elementów SA,B =
2. Ile elementów ma zbiór SA,B, gdy:
a) A = {1, 2, 3}, B = {11, 12, 13, 14, 15, 16, 17, 18} , liczba elementów SA,B =
b) A = {-2, -1, 0, 1, 2}, B = {111, 112, 113, 114, 115, 116, 117} liczba el. SA,B =
c) A = {-2, -1, 0, 1, 2}, B = {1, 2, 3, 4, 5, 6, 7} , liczba elementów SA,B =
d) A = {-3, -2, -1, 0, 1, 2, 3}, B = {-3, -2, -1, 0, 1, 2, 3} , liczba elementów SA,B =
3. Podaj (o ile istnieje) przykład zbioru oraz określ, ile jest takich zbiorów B, że:
a) A = {1, 3, 5}, SA,B = {9, 10, 11} , np. B = wszystkich jest
b) A = {1, 3, 5}, SA,B = {9, 10, 11, 12, 13} , np. B = wszystkich jest
c) A = {9, 10, 11, 12, 13}, SA,B = {1, 2, 3} , np. B = wszystkich jest
d) A = {-2, 0, 2}, SA,B = {11, 12, 13, 14, 15, 16} np. B = wszystkich jest
4. Uzupełnij (kratka na rysunkach ma wymiary 1 ×1):
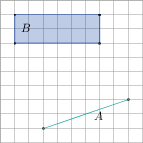 liczba boków SA,B = pole SA,B = |
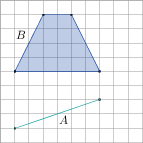 liczba boków SA,B = pole SA,B = |
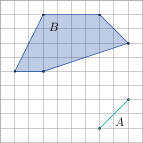 liczba boków SA,B = pole SA,B = |
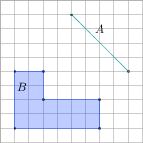 liczba boków SA,B = pole SA,B = |
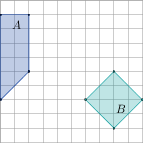 liczba boków SA,B = pole SA,B = |
 liczba boków SA,B = pole SA,B = |
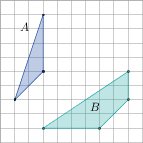 liczba boków SA,B = pole SA,B = |
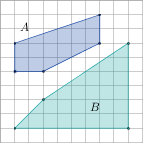 liczba boków SA,B = pole SA,B = |
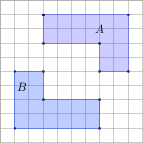 liczba boków SA,B = pole SA,B = |
5.
W sześcianie KLMNK'L'M'N' krawędzie są długości 8 cm.
Jaki kształt i wymiary ma SA,B, gdy:
a)
A jest krawędzią KK' i B jest krawędzią LM?
Odpowiedź:
b)
A jest krawędzią KK' i B jest ścianą LMM'L?
Odpowiedź:
c)
A jest krawędzią KK' i B jest ścianą KLMN?
Odpowiedź:
d*)
A jest odcinkiem K'M' i B jest trójkątem KLM?
Odpowiedź:
i
4 e*)
A jest odcinkiem KM' i B jest trójkątem LMN?
Odpowiedź:
).
f**)
A jest czworościanem KLNK' i B jest
czworościanem L'M'N'M ;
Dla SA,B podaj, ile ma:
wierzchołków
,
krawędzi:
,
ścian:
.
SA,B ma objętość
i pole powierzchni równe
6*. Jaki kształt i wymiary ma SA,B, gdy:
a)
A jest kwadratem KLMN o boku 2 i B jest prostą równoległą do KL odległą o 8 od środka kwadratu?
Odpowiedź:
b)
A jest trójkątem równobocznym KLM o boku 4 i B jest prostą równoległą do KL odległą o 8 od środka trójkąta?
Odpowiedź:
7*. Uzupełnij (kratka na rysunkach ma wymiary 1 ×1):
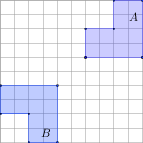 liczba boków SA,B = pole SA,B = |
 A jest łamaną, B - kołem pole SA,B = |
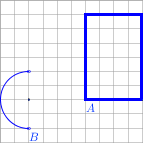 A jest łamaną, B - półokręgiem pole SA,B = |
Warto przeczytać inne teksty o podobnej tematyce:
- Środki zbiorów liczb
- Odcinek figur
- Środki figur płaskich
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
