Środki zbiorów liczb

Liczba 4,5 leży dokładnie w połowie odległości między 2 i 7. Jest środkiem odcinka o końcach 2 i 7 na osi liczbowej. Jak obliczyć, gdzie znajduje się środek odcinka między dwoma liczbami na osi? Do mniejszej z nich należy dodać połowę odległości między nimi, czyli w naszym przypadku 4,5 = 2 + ^. (7 - 2) = ^. 2 + ^. 7 = ^. (2 + 7).
 
Ogólnie liczba (x + y) = x + y  leży na osi liczbowej dokładnie w środku pomiędzy różnymi liczbami x, y. Sprawdź rachunki podobne jak poprzednio dla x < y.

 

Określenie 1
Dla zbioru liczbowego A niech S_A oznacza zbiór wszystkich środków odcinków o końcach ze zbioru A. Będziemy mówili, że S_A jest środkiem zbioru A.

 

Przykład 1.   Dla zbiorów skończonych łatwo jest wyliczyć ich środki (może to być co najwyżej żmudne):

    Dla  A = {1, 5, 6}  mamy   S_A  =  { (1+5), (1 + 6), (5 + 6)}  =  {3, 3, 5}.

    Dla  A = {1, 2, 3, 5}  mamy   S_A  =  {1, 2, 2, 3, 3, 4}.

    Dla  A = {4, 8, 12}  mamy   S_A  =  {6, 8, 10}.

      S_{{10, 100, 1000, 1000000}}  =  {55, 505, 550, 500005, 500050, 500500} .

 

Przykład 2.   Dla przedziałów i sum przedziałów problem jest nie tylko z końcami.

    Dla przedziału domkniętego  [2, 5]  mamy   S_{[2, 5]}  =  (2, 5) = S_{(2, 5)}. Dlaczego?

    Dla sumy przedziałów  A = [2, 5] [6, 8]   mamy   S_A  =  (2, 8). Dlaczego?

    Dla  A = [2, 5] [7, 9]   mamy   S_A  =  (2, 9). Dlaczego?

    Dla  A = [2, 5] [7, 9)   mamy   S_A  =  (2, 7) (7, 9) = (2, 9) \ {7}. Dlaczego?

    Dla  A = [2, 5] (17, 19]   mamy   S_A  =  (2, 5) (9,5, 12] (17, 19). Dlaczego?

 

Przykład 3.       Dla zbioru liczb wymiernych  W  mamy   S_W  =  W .
Tak jest, bo:
-    po pierwsze:   suma i iloraz liczb wymiernych są liczbami wymiernymi, więc (x + y) - środek pary liczb wymiernych x, y, jest liczbą wymierną,
-    po drugie:   gdy x jest liczbą wymierną, to x = ((x-1) + (x+1)), czyli jest środkiem odcinka o końcach wymiernych: x-1 i x+1 .

 

Przykład 3'.       Dla zbioru liczb niewymiernych  R \ W  mamy   S_{R \ W}  =  R.
Tak jest, bo:
-   gdy x jest liczbą wymierną, to x jest środkiem odcinka o końcach niewymiernych: x- i x+,
-  gdy x jest liczbą niewymierną, to x jest środkiem odcinka o końcach niewymiernych: x-1 i x+1.

 

Przykład 4.   Niech U₂ oznacza zbiór wszystkich ułamków właściwych (z przedziału (0, 1)), których mianowniki są potęgami dwójki.

    Dla  U₂ = { ¹/₂, ¹/₄, ³/₄, ¹/₈, ³/₈, ⁵/₈, ⁷/₈, ¹/₁₆, ³/₁₆, . . . } .   mamy   S_U2 = U₂.
Żeby to uzasadnić, pokażemy, że:
  a)   środek każdej pary liczb x, y z U₂ należy do U₂ ,
  b)   każda liczba u z U₂ jest środkiem pewnych dwóch liczb należących do U₂.
Ad. a) 
Ad. b) 

 

Przykład 5.   Niech U₁₀ oznacza zbiór wszystkich ułamków właściwych (z przedziału (0, 1)), których mianowniki są potęgami 10.

    Czy dla  U₁₀   mamy   S_U10 = U₁₀?    Tak.
Można uzasadniać podobnie jak w poprzednim przykładzie.
Można też stwierdzić:
'U₁₀ to są wszystkie liczby z (0,1) o skończonych rozwinięciach dziesiętnych.
Teza jest oczywista - pomyśl o działaniach pisemnych: dodawaniu, dzielenie przez 2.' .

 

---

 

Dalsze przykłady są ciekawsze (ale trudniejsze).

 

Przykład 6.   Niech B₅ oznacza zbiór wszystkich liczb z przedziału [0, 1], które można zapisać w układzie dziesiętnym bez cyfry 5.
Do B₅ nie należy żadna liczba z przedziału otwartego (0,5, 0,6), ale 0,5 jest w B₅,
bo 0,5 = 0,4(9) - nawias oznacza, że cyfra dziewięć jest w okresie.
Przybliżenie zbioru B₅ jest pokazane na poniższym rysunku.

Zobaczmy, że

S_B5 = (0, 1), każda liczba x z przedziału (0, 1) jest środkiem odcinka o końcach x', x'' zapisanych bez cyfry 5.

Dla konkretnych przykładów x nie jest trudno podać odpowiednie x', x'', np.:

x = 0,230521541... = (0,130421441... + 0,330621641...),
x = 0,909012273... = (0,869012273... + 0,949012273...). Jednak ogólny przepis jest dość zawiły, bo trzeba rozpatrzyć różne przypadki.
 
Niech 0,c₁c₂c₃ oznacza zapis dziesiętny liczby x. Tworzymy nowe dwie liczby x' < x'' o zapisach dziesiętnych x' = 0,b₁b₂b₃... i x'' = 0,d₁d₂d₃..., według następującego przepisu:
  -   gdy w zapisie x występuje cyfra 4, 5 lub 6, to b_i = c_i-2, d_i = c_i+2 gdy c_i jest równe 4, 5 lub 6 oraz b_i = d_i = c_i w pozostałych przypadkach,
  -   gdy w zapisie x nie występują cyfry 4, 5 i 6, ale jest jakaś cyfra c_io równa 1, 2, 3, 7 lub 8,
to b_io = c_io-1, d_io = c_io+1 oraz b_i = d_i = c_i dla i i_o ,
  -   gdy w zapisie x są same cyfry 0 i 9 i jest takie i_o, że c_io = 9, c_io+1 = 0, to b_io = 8, b_io+1 = 6, d_io = 9, d_io+1 = 4 oraz b_i = d_i = c_i dla i i_o oraz i i_o+1,
  -   gdy w zapisie x są same cyfry 0 i 9 i nie ma takiego i_o, że c_io = 9, c_io+1 = 0, to x ma inne, skończone rozwinięcie dziesiętne; dla niego tworzymy x', x''według jednej z powyższych reguł.

Tak utworzone liczby x', x'' są zapisane bez cyfry 5, są z przedziału [0, 1], x' < x''
oraz x = (x' + x''), co nie jest trudne do sprawdzenie, jeśli pomyślimy o pisemnym dodawaniu (wykonywanym 'od lewej do prawej').

 

Przykład 6'.   Niech B_4,5 oznacza zbiór wszystkich liczb z przedziału [0, 1], które można zapisać w układzie dziesiętnym bez cyfr 4 i 5.
Do B_4,5 nie należy żadna liczba z przedziału (0,4, 0,6), ale 0,4 jest w B_4,5, bo 0,4 = 0,3(9). Przybliżenie zbioru B_4,5 jest pokazane na poniższym rysunku.

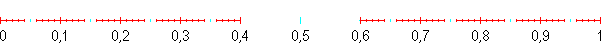
Podobnie jak w poprzednim przykładzie można pokazać, że

S_B4,5 = (0, 1), każda liczba x z przedziału (0, 1) jest środkiem odcinka o końcach zapisanych bez cyfr 4 i 5.

 

Przykład 6''.   Niech B_3,4,5,6 oznacza zbiór wszystkich liczb z przedziału [0, 1], które można zapisać w układzie dziesiętnym bez cyfr 3, 4, 5 i 6.
B_3,4,5,6 powstaje z przedziału [0, 1], z którego usuwamy kolejno przedziały otwarte:
    (0,3, 0,7),
    (0,03, 0,07), (0,13, 0,17), (0,23, 0,27), (0,73, 0,77), (0,83, 0,87), (0,93, 0,97),
    i dalsze: (0,003, 0,007), (0,013, 0,017), ...
i tak 'w nieskończoność'. To, co zostanie, to właśnie zbiór B_3,4,5,6.
Mamy

S_B3,4,5,6 (0, 1), bowiem 'dziury' są za szerokie, np. żadna liczba z przedziału (0,65, 0,7] nie jest środkiem odcinka o końcach zapisanych bez cyfr 3, 4, 5 i 6.

 

Przykład 7.   Interesującą własność ma zbiór B₈ wszystkich liczb z przedziału [0, 1], które można zapisać w układzie dziesiętnym bez cyfry 8. Do B₈ nie należy żadna liczba z przedziału otwartego (0,8, 0,9). Podobnie jak w przykładzie 6. można pokazać, że

S_B8 = (0, 1), tzn. każda liczba x z przedziału (0, 1) jest środkiem odcinka o końcach zapisanych bez cyfry 8.
 
Ciekawe jest to, że niektóre z liczb z przedziału (0, 1) są środkami dokładnie jednego odcinka o końcach w B₈, na przykład liczby: 0,9 = (0,7(9) + 0,(9)),
0,99 = ( 0,97(9) + 0,(9)),
0,999 = ( 0,997(9) + 0,(9)). Są to jedyne przedstawienia tych liczb, gdzie po prawej stronie w nawiasie są liczby z B₈, bo 'dziury' z lewych stron tych liczb są takie, jak ich odległości od 1.
 
Jest jednak wiele liczb bez tej jednoznaczności, na przykład: 0,5 = (0,4 + 0,6) = (0,3 + 0,7),
0,(3) = (0,(4) + 0,(2)) = (0,(5) + 0,(1)).

 

Przykład 8.   Zbiór Cantora C, to zbiór wszystkich liczb z przedziału [0, 1], które można zapisać w układzie trójkowym bez cyfry 1. Do C nie należy żadna liczba z przedziałów otwartych:
                                                               (¹/₃, ²/₃),
                           (¹/₉, ²/₉),                                                            (⁷/₉, ⁸/₉),
      (¹/₂₇, ²/₂₇),                    (⁷/₂₇, ⁸/₂₇),                     (¹⁹/₂₇, ²⁰/₂₇),                 (²⁵/₂₇, ²⁶/₂₇),
(¹/₈₁, ²/₈₁),   ...                     

Przybliżenie zbioru C jest pokazane na poniższym rysunku. Podpisy są w układzie trójkowym.

Metodami z poprzednich przykładów, rachując w układzie trójkowym, można pokazać, że:

S_C (0, 1),

że do zbioru S_C należą te i tylko te liczby, które należą do przedziałów domkniętych:
                                                               [¹/₃, ²/₃],
                           [¹/₉, ²/₉],                                                            [⁷/₉, ⁸/₉],
       [¹/₂₇, ²/₂₇],                     [⁷/₂₇, ⁸/₂₇],                      [¹⁹/₂₇, ²⁰/₂₇],                [²⁵/₂₇, ²⁶/₂₇],
[¹/₈₁, ²/₈₁],   ...                     
Przy czym tylko końce tych przedziałów, czyli liczby: ¹/₃, ²/₃, ¹/₉, ²/₉, ⁷/₉, ⁸/₉, ¹/₂₇, ²/₂₇, ⁷/₂₇, ⁸/₂₇, ¹⁹/₂₇, ²⁰/₂₇, ²⁵/₂₇, ²⁶/₂₇, ¹/₈₁, ²/₈₁, ... (tzn. liczby z (0, 1) o skończonych rozwinięciach trójkowych) mają jednoznaczne przedstawienia jako środki odcinków o końcach w C.

 

---

---

 

Określenie 2
Zbiór G nazywamy generatorem zbioru A, gdy G jest podzbiorem A, S_G = S_A oraz

dla każdego x z S_A istnieje dokładnie jedna para x'< x'' liczb z G taka, że x = (x' + x'').

 

Na koniec poznamy trzy twierdzenia, które mówią, że dla pewnych zbiorów ISTNIEJĄ ich generatory. To dość nietypowe twierdzenia, bo mówią o ISTNIENIU generatorów, ale nie pokazują, jak te generatory wyglądają. Tego typu twierdzenia noszą nazwę twierdzeń egzystencjalnych i w początkach XX wieku budziły sporo kontrowersji.
Po co dowodzić ISTNIENIA, kiedy wydaje się, że o wiele lepiej i łatwiej jest po prostu WSKAZAĆ lub SKONSTRUOWAĆ przykład. Tyle, że czasami nie wiadomo JAK.

 

Twierdzenie 1 
Istnieje generator zbioru U₂ ułamków właściwych o mianownikach będących potęgami 2.

 

Dowód 
Na początek ponumerujmy wszystkie elementy S_U2 = U₂ : u₁ = , u₂ = , u₃ = i dalej jakkolwiek (byle różnowartościowo): u₄, u₅,... . Niech G₁ = {u₂, u₃} = {, }.

Przypuśćmy, że dla ustalonej liczby naturalnej n mamy skończone zbiory G₁, G₁, ..., G_n. Tworzymy teraz nowy zbiór G_n+1.

Jeśli u_n+1 jest w S_Gn, to niech G_n+1 = G_n. Dalej rozpatrujemy przypadek gdy u_n+1 nie jest w S_Gn.

Utwórzmy pomocniczy zbiór P_n liczb postaci p, q-p, q+r-p, gdzie p, q, r są w G_n{u_n+1}.
P_n ma skończenie wiele elementów, bo skończony jest zbiór G_n {u_n+1}.
Zatem wśród nieskończenie wielu par liczb x' < x'' z U₂, dla których u_n+1 = (x' + x''),
istnieje taka, że x', x'' i x' - x'' nie są w P_n.
Stąd już wynika (sprawdź prostymi rachunkami), że dla wszystkich p, q, r z G_n zachodzi

(x' + p) (x'' + q),
(x' + p) (x' + x''),     (x'' + p) (x' + x''),
(x' + p) (q + r),     (x'' + p) (q + r) . Określamy G_n+1 = G_n {x', x''}.
Oczywiście u_n+1 = (x' + x'') jest w zbiorze S_Gn+1.
Oczywiście G_n+1 jest skończonym zbiorem o elementach z U₂, o ile G_n ma tę własność.
Powyższe nierówności gwarantują, że środki G_n+1 są wyznaczane jednoznacznie, tzn. (y' + y'') (z' + z''),   dla dowolnych dwóch różnych par y' < y'' i z' < z'' z G_n+1, o ile G_n ma tę własność, tzn. o ile (y' + y'') (z' + z'') ,   dla dowolnych dwóch różnych par y' < y'' i z' < z'' z G_n.

Na mocy twierdzenia o indukcji matematycznej można 'wymazać' owe o ile. Istnieje nieskończony ciąg zbiorów G₁, G₂, G₃,..., takich, że dla każdego naturalnego k:
(i)    G_k jest skończonym podzbiorem U₂,
(ii)    u_k jest w S_Gk,
(iii)    środki G_k są wyznaczone jednoznacznie przez elementy z G_k.

Na koniec niech G oznacza zbiór wszystkich liczb ze zbiorów G₁, G₂, G₃,... (w nieskończoność).
Sprawdzimy, że G jest generatorem.
  -   własność (i) gwarantuje, że G U₂, skąd mamy S_G S_U2 = U₂,
  -   własność (ii) gwarantuje, że U₂ S_G, zatem  S_G = S_U2 = U₂,
  -   środki G są wyznaczone jednoznacznie przez elementy z G .
Niech bowiem (a + b) (c + d),  dla pewnych par a < b i c < d z G.
Istnieją liczby naturalne k_a, k_b, k_c, k_d takie, że a jest w G_ka, b w G_kb, c w G_kc, d w G_kd.
Dla k będącego największą z liczb k_a, k_b, k_c, k_d, liczby a, b, c, d są z G_k.
Zatem, z własności (iii), pary a < b i c < d są jednakowe.

 

Uwaga 1.  Istnieje wiele różnych generatorów zbioru U₂, bo w dowodzie braliśmy jakąś  spośród nieskończenie wielu par liczb x' < x'' i można zadbać, by jakaś ustalona liczba nigdy nie była wybrana.

 

Uwaga 2.  Każdy generator G jest minimalny, tzn. odrzucenie choć jednego jego elementu x spowoduje, że przestanie być generatorem, bowiem   S_G\{x} S_G. Dlaczego?
Należy odróżnić pojęcie minimalny od najmniejszy. Nie ma najmniejszego generatora, bo nie ma generatora zawartego w każdym innym. Dlaczego?

 

Uwaga 3.  W dowodzie braliśmy nieskończenie wiele razy jakieś pary liczb x' < x''. Można powiedzieć, że nieskończenie wiele razy wybieraliśmy. Poprawność takiego postępowania, tzn. możliwość 'nieskończonego wybierania jakichś elementów', jest gwarantowana przez tzw. AKSJOMAT WYBORU. Mówi on, że takie postępowanie jest poprawne. To stwierdzenie zazwyczaj przyjmuje się jako aksjomat (= bez dowodu) przy budowaniu wielu teorii matematycznych.

 

Dowód poniższego twierdzenia niemal niczym nie różni się od poprzedniego dowodu, należy tylko jakoś ponumerować elementy zbioru   S_{(0, 1) W}  =  (0, 1) W.

 

Twierdzenie 2. 
Istnieje generator zbioru (0, 1) W, tzn. zbioru liczb wymiernych z przedziału (0, 1).

 

Ponieważ wszystkich liczb z (0, 1) nie można ponumerować liczbami naturalnymi, więc poprzednia metoda dowodzenia nie może być wprost zastosowane w dowodzie poniższego twierdzenia.

 

Twierdzenie 3 
Istnieje generator zbioru (0, 1).

 

Uwaga 4. (tylko dla dorosłych)  W XX wieku w matematyce wprowadzono liczby porządkowe (uogólnienie liczb naturalnych), którymi można 'ponumerować' wszystkie liczby z przedziału (0, 1). Uogólniono też zasadę indukcji matematycznej na stwierdzenia zależne od liczb porządkowych. Dzięki temu dowód twierdzenia 1 da się 'przepisać' niemal bez zmian tak, by stał się dowodem twierdzenia 3. Należy tylko zamiast 'skończony', pisać: 'mocy mniejszej od continuum'; zamiast 'nieskończony', pisać 'mocy równej continuum' (i (0,1) w miejsce U₂).

 

Uwaga 5.  Może rozważania o aksjomacie wyboru i twierdzeniach egzystencjalnych są zbędne. Może da się 'jawnie' wskazać generator zbioru liczb (0, 1)? Ja nie umiem, ale może któryś z Czytelników znajdzie prosty dowód.

 

---

---

 

Warto przeczytać inne teksty o podobnej tematyce:
   - Środki par zbiorów
   - Odcinek figur
   - Środki figur płaskich

 

---

---

---