Światowidy dyskretne

Do rysunków 3D w niebieskich ramkach użyto apletu www.javaview.de/ Można w nich manipulować myszą.

 

Każda z poniższych brył wygląda jak mityczny Światowid, czyli posąg o czterech jednakowych twarzach patrzących w cztery strony świata. Rzeczywiście, każda z tych brył oglądana z każdej z czterech stron świata wygląda jednakowo. Zobacz.

 

Zapraszamy do zabawy w projektowanie własnych światowidów.
Na siatce n×n wyklikaj swój projekt P, t.j. widok z profilu (lub 'en face', bo są jednakowe) projektowanej bryły.
Automat z sześcianu n×n×n

wytnie te i tylko te bloki, które są zbędne. Jak mówił Michał Anioł: 'Rzeźbi Natura, ja tylko usuwam to, co zbędne'.

Pracownia projektowa światowidów
 

 

 
Uwaga 1 
Dla danego projektu P jest (zazwyczaj) wiele brył, które oglądane z czterech stron wyglądają jednakowo, tak jak P. Wśród nich są takie, które składają się z tylu bloków, z ilu kratek składa się P (b=p). Najprostsza z nich jest ustawiona nad przekątną podstawy sześcianu (zobaczysz ją na prawym rysunku, gdy odhaczysz opcję [max/min]). Jednak rzeźbiąc takie bryły, usuwamy za dużo bloków, również te, które nam nie przeszkadzają, bo nie psują projektu P.
Dalej będziemy zajmować się tylko tymi bryłami, które powstały według algorytmu:

z sześcianu n×n×n usuwamy te i tylko te bloki, które są zbędne. To tak, jakby kwadratowym dłutem przebijać sześcian na wylot w miejscach, które na projekcie P nie są zaznaczone. Tylko takie bryły nazwiemy światowidami. Tylko one są wyświetlane powyżej (zaznacz opcję [max/min]).

 
Uwaga 2 
Gdy projekt P nie jest symetryczny, można mieć wątpliwości, czy światowid z każdej strony wygląda jednakowo, bo na przykład z przodu macha prawą ręką, a gdy patrzymy od tyłu - macha lewą. Tak już musi być. Podobnie jest podczas oglądanie się w lustrze. Zatem słowo 'jednakowe' oznacza tu 'identyczne' albo 'będące odbiciem symetrycznym' (względem płaszczyzny).

 
Uwaga 3 
Gdy projekt P nie jest symetryczny, można zobaczyć, że jest kilka sposobów usuwania zbędnych bloków. Drugi sposób zobaczysz, zaznaczając opcję [sym]. Wtedy uzyskasz odbicie symetryczne światowida. Względem jakiej płaszczyzny?

 

---

 

Zadanie 1.   Dla podanego projektu P wyobraź sobie całego światowida i oblicz:
   -  pole p projektu P (jednostką jest kratka),
   -  liczbę b bloków, z których składa się cała rzeźba,
   -  pole ś całej rzeźby, nie zapomnij o polu 'od spodu' (jednostką jest kratka).
W powyższych podpunktach spróbuj wyznaczyć ogólne wzory w zależności od wymiaru siatki n.

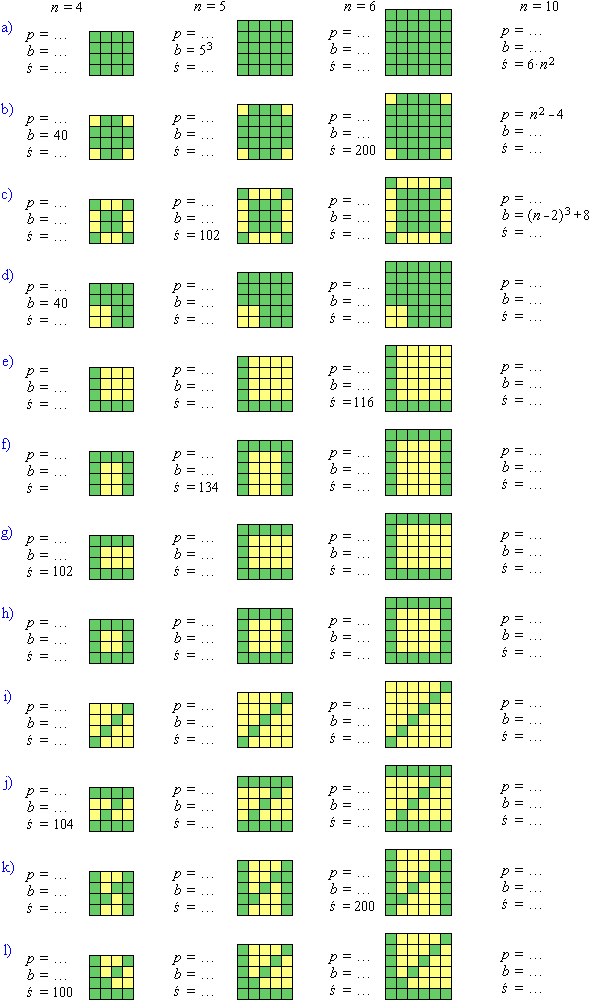
Teraz podamy jeszcze trzy trudniejsze przykłady. Ostatni wymyśl samodzielnie.

 

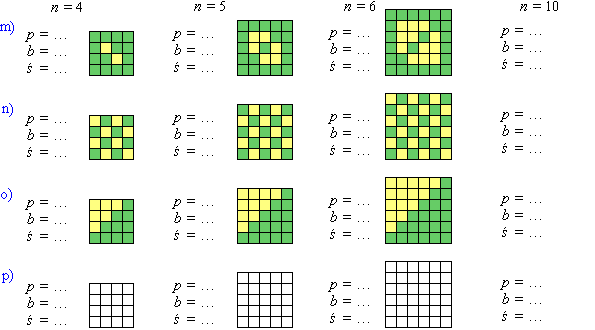
Zadanie 2.   Odpowiedz na poniższe pytania, gdy n = 5, to znaczy, gdy światowidy projektowane są na siatce 5 × 5.
a)  Ile jest wszystkich światowidów, których pole ś = 6 [kratek]?   45
b)  Ile jest wszystkich światowidów, których pole ś = 7 [kratek]?   0, nie ma takich.
c)  Ile jest wszystkich światowidów, których pole ś = 8 [kratek]?   0, nie ma takich.
 
A jak jest ogólnie, to znaczy gdy światowidy projektowane są na siatce n×n?

 

Zadanie 3.   W Zadaniu 1. w każdym przykładzie ś jest liczbą parzystą. Czy tak jest zawsze?
 
Wskazówka.  Tak jest dla każdej bryły zbudowanej z sześciennych bloków łączonych całymi ścianami, nie tylko dla światowidów.

 

Zadanie 4.   Wiadomo, że projekt P na siatce 4 × 4 ma:
  -   w dolnym wierszu 3 zaznaczone kratki,
  -   w następnym wierszu ma 4 zaznaczone kratki,
  -   w kolejnym - 2 kratki
  -   w najwyższym - 1 kratkę.
Czy na podstawie tych informacji można obliczyć:
a)  liczbę bloków b?   Tak. Oblicz.
b)  pole ś ?   Nie. Podaj dwa przykłady o różnych wartościach ś.

 

Zadanie 5.   W Zadaniu 1. w niektórych przykładach mamy:

ś  =  2n² + 4 p . W których?

 

---

 

Zależność: ś  =  2n² + 4 p jest dość ciekawa.
Spróbujmy zobaczyć, dla jakich projektów P ona zachodzi.
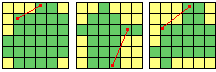W pierwszej chwili może wydawać się, że ma to związek z wypukłością figury P.
I tak, i nie.
Nie, bo dla każdego projektu z rysunku obok zachodzi ta zależność, a żaden z tych projektów nie jest figurą wypukłą (co pokazują czerwone odcinki).
Jednak ma to związek z pewną odmianą wypukłości.

Powiemy, że figura (płaska) P jest poziomo wypukła, gdy każda prosta pozioma, która przecina P, przecina P wzdłuż odcinka.

To jeszcze nie wystarcza.

Może wydawać się, że:

jeśli figura P jest poziomo i pionowo wypukła,
to zachodzi związek: ś  =  2n² + 4 p .

To dalej nie jest poprawne. Dlaczego?

Poprawnie (ale niezbyt precyzyjnie) można powiedzieć:

jeśli figura (kratkowa) P jest poziomo i pionowo wypukła
i pewne poziome cięcie ma długość n,
to zachodzi związek: ś  =  2n² + 4 p.

Zamiast precyzować to sformułowanie, lepiej zajrzeć do wytwórni światowidów super3D.

A jeśli chcesz dowiedzieć się, jak obliczać objętości brył-światowidów, zajrzyj do tekstu Światowidy wielościenne.

 

---

---