Jak zbudować sześcian z deseczek?
Wydaje się to bardzo proste: wystarczy wyciąć sześć kwadratów, skleić i po problemie.
A jednak problem jest.
Popatrz na sześć jednakowych deseczek o wymiarach 10 cm × 10 cm × 0,4 cm.
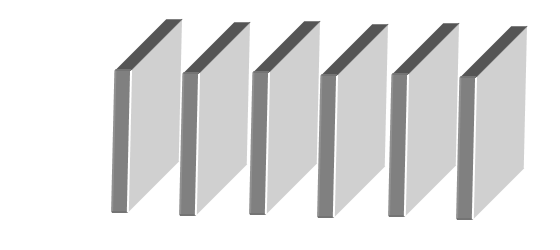
Cztery deseczki można skleić łatwo.
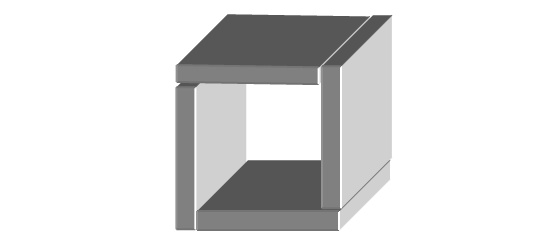
Jednak piąta (i szósta) nie pasują!
Zobacz, że są za małe.
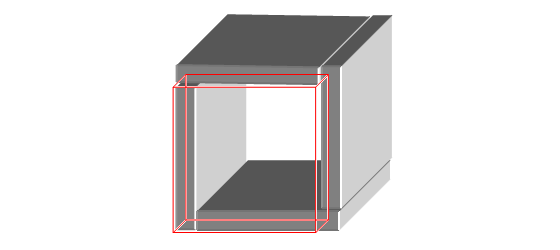
Może trzeba inaczej zacząć sklejanie?
Spróbuj.
Zapewne stwierdziłeś, że to się nie może udać.
Po wielu próbach nie udało się skleić z tych deseczek sześcianu.
Ale to, że nie umiesz go skleić, wcale nie oznacza, że nie da się tego zrobić!
Może komuś innemu jednak się udało?
Jak przekonać się, czy rzeczywiście się nie da? Jak uzasadnić, że tego żadnym sposobem nie można zrobić?
Przypuśćmy, że z sześciu jednakowych deseczek o wymiarach 10 cm × 10 cm × 0,4 cm można jednak skleić sześcian.
Taki (hipotetyczny) sześcian miałby krawędź długości
Zatem taki (hipotetyczny) sześcian miałby pole powierzchni
Na styku sąsiednich deseczek jedna z cienkich ścianek jest schowana, a druga jest na powierzchni sześcianu. Zatem łączne pole powierzchni deseczek na powierzchni sześcianu jest równe
Jest to inna liczba niż te wypisane wcześniej.
Zatem otrzymaliśmy sprzeczność z przypuszczeniem, że taki sześcian istnieje.
Powyższe rozumowanie jest właśnie szukanym dowodem. Uzasadnia, że z takich deseczek nie można skleić sześcianu.
Nie oznacza to jednak, że nie można w ogóle zrobić sześcianu z sześciu deseczek.
Można przecież wyciąć niejednakowe deseczki (jakie?) i z nich skleić sześcian.
Można też deseczki spiłować wzdłuż krawędzi, tak jak na rysunku poniżej.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
