W pełni symetryczne zamalowane plansze

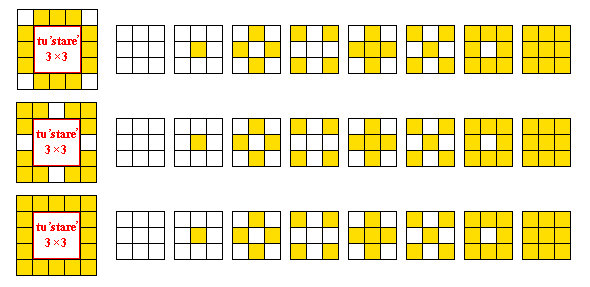
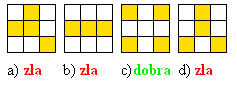Na rysunku obok są cztery pokolorowane kwadratowe szachownice rozmiaru 3×3. Tylko plansza c) jest w pełni symetryczna.
Plansza b) nie jest symetryczna względem przekątnej kwadratu, podobnie jak plansza d).
 

Nietrudno jest narysować wszystkie w pełni symetryczne pokolorowane plansze 3×3.
Jak to zrobić systematycznie, aby nie pominąć żadnej i uniknąć powtórzeń?

Można je na przykład uporządkować ze względu na liczbę zamalowanych pól:

liczba zama- lowanych pól	0	1	2	3	4	5	6	7	8	9
plansze		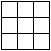	brak	brak			brak	brak

Zauważmy, że każda plansza ma swojego 'bliźniaka', np.:
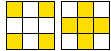
Bliźniacy mają zamienione miejscami pola białe i zamalowane.

To spostrzeżenie pozwala w powyższej tabeli automatycznie wypełnić kolumny od 5 do 9.
Każda plansza o liczbie zamalowanych pól większej od 4 ma bliźniaka o liczbie zamalowanych pól mniejszej od 5.

Z uwagi na tę własność uznajemy planszę białą jako w pełni symetryczną, bo jest bliźniacza do tej o wszystkich polach zamalowanych.

Jest 8 w pełni symetrycznych plansz 3×3, co zanotujmy jako   p₃ = 8.

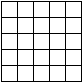Rozważmy teraz w pełni symetryczne zamalowane kwadratowe plansze rozmiaru 5×5.
Jak narysować je wszystkie?
Jak to robić, aby nie pominąć żadnej i uniknąć powtórzeń?

Poprzedni pomysł plansz bliźniaczych teraz również działa, ale nie upraszcza zbytnio problemu.

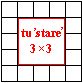Nowy pomysł widać na rysunku obok. Plansze 5×5 mają w środku plansze 3×3, wokół których jest ramka. Kolorowanie ramki i środka jest niezależne, to znaczy
dla każdego w pełni symetrycznego pokolorowania ramki środek można wypełnić jedną z w pełni symetrycznych plansz 3×3.

Z tego można już wywnioskować, że liczba p₅ wszystkich w pełni symetrycznych plansz 5×5 jest podzielna przez 8 = p₃.

Zatem można zająć się tylko kolorowaniem ramki.

To jeszcze nie wszystkie plansze. Jakie są pozostałe?

Rozważmy teraz w pełni symetryczne zamalowane kwadratowe plansze rozmiaru 7×7.

Do narysowania wszystkich można wykorzystać poprzedni pomysł ramek i środków.

Dokonajmy jednak jeszcze innej obserwacji.
Pstrokata plansza obok pokazuje zależności między polami.
Na przykład popatrzmy na jasnozielone pola.
Muszą być zamalowane albo wszystkie, albo żadne z nich.
Podobnie jest z polami innych kolorów. Wynika to z pełnej symetrii plansz.

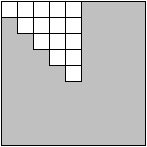
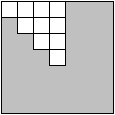Wystarczy patrzeć na niektóre z pól, na przykład na te z rysunku obok.
Nazwijmy je generatorami. Zanotujmy: g₇ = 10.
Można zasłonić resztę planszy, a stan zamalowania generatorów zdeterminuje stan wszystkich pozostałych pól planszy.

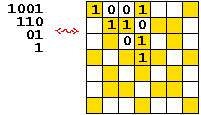
Zamiast całych plansz można notować układy 0 i 1,
jak pokazuje przykład obok.

Połączmy dotychczasowe obserwacje. Obliczmy, ile jest wszystkich w pełni symetrycznych plansz 7×7. Ile wynosi p₇?

          0001
          0010
          0011
          0100
          0101
          0111
           1000
           1001
           1010
           1011
           1100
           1101
           1110
           1111

 
 
Dalej obliczymy p₉ - liczbę wszystkich w pełni symetrycznych zamalowanych plansz 9×9.
Ramki tych plansz są zakodowane przez układy 5 generatorów.
Kody tych ramek dzielą się na dwie grupy:
   -   zaczynające się od 0,
   -   zaczynające się od 1.
Każdego typu jest tyle, ile wszystkich ramek poprzednich, czyli 16.
Teraz każdą z 2^.16 ramek wypełniamy dowolną planszą 7×7, czyli

p₉ = 2^.16 ^. p₇ = 32 ^. 1024 = 32768.

 
 
Tak samo oblicza się p₁₁.
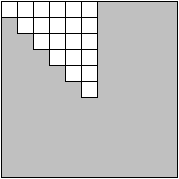
Ramki plansz 11×11 są zakodowane przez układy 6 generatorów.
Kody tych ramek dzielą się na dwie grupy:
   -   zaczynające się od 0,
   -   zaczynające się od 1.
Każdego typu jest tyle, ile wszystkich ramek poprzednich, czyli 32.
Potem każdą z 2^.32 ramek wypełniamy dowolną planszą 9×9, czyli

p₁₁ = 64 ^. p₉ = 64 ^. 32768 = 2097152.

Zadanie 1 
Zbadaj w pełni symetryczne zamalowane kwadratowe plansze:
   a)    4×4,
   b)    6×6,
   c)    8×8.
Oblicz, ile ich jest. Oblicz wielkości p₄, p₆, p₈.
Wskazówka. p₈ = p₇. Dlaczego?  

Zadanie 2 
Zbadaj w pełni symetryczne zamalowane plansze typu:

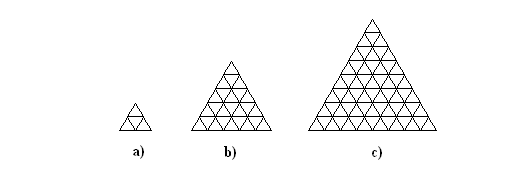
Oblicz, ile ich jest.

Zadanie 3 
Zbadaj w pełni symetryczne zamalowane plansze typu:

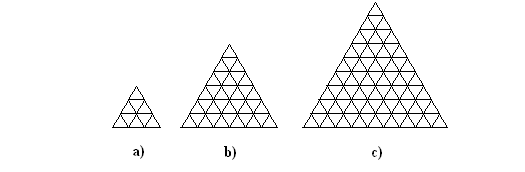
Oblicz, ile ich jest.

Zadanie 4 
Zbadaj w pełni symetryczne zamalowane plansze typu:

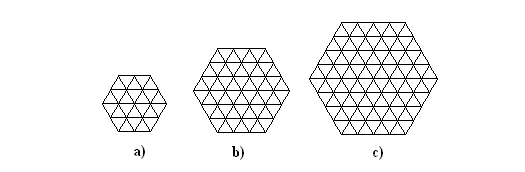
Oblicz, ile ich jest.