| więcej informacji o tekście: |
Gdy pinezką P przyszpilimy figurę wyciętą z kartonu, aż prosi się, by nią zakręcić. Co wtedy widać? Wiatraczek. Pisaliśmy już o nim w artykule Z pinezką (rzeczywistą i urojoną) - warto zacząć od przeczytania tego tekstu.
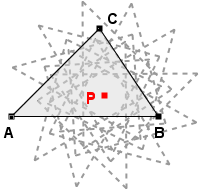
Wiatraczek z rysunku obok częściowo zasłania to, co znajduje się za nim. Tuż przy pinezce zasłania wszystko dokładnie, a im bliżej brzegu, tym jest bardziej przezroczysty. Można powiedzieć, że jego gęstość maleje, gdy rośnie odległość od pinezki.
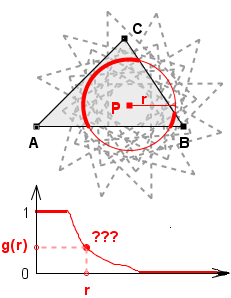
Co to jest gęstość wiatraczka?
Przyjmiemy, że:
w odległości r od pinezki gęstość g(r) podaje, jaka część okręgu o promieniu r i środku P jest zawarta w figurze.
Zatem gęstość wiatraczka jest funkcją, która liczbie dodatniej r przypisuje wartość g(r) równą ilorazowi długości części okręgu o(P,r) zawartej w figurze i długości całego okręgu.
Wyraźnie podkreślmy: gęstość zależy i od kształtu figury, i od położenia pinezki.
Nim podamy wzory na gęstości niektórych wiatraczków,
omówimy pewne własności, które nie wymagają rachunków.
Będziemy starali się opisać, jak wyglądają wykresy gęstości.
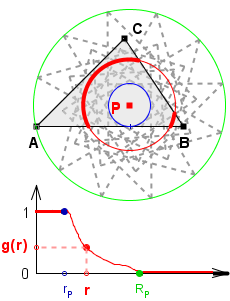
Funkcja g(r) przyjmuje wartości z przedziału [0,1].
Gdy rP i RP
oznaczają promień wewnętrzny i zewnętrzny (pojęcia omawiane w
tekście Z pinezką...), to:
dla 0 < r < rP mamy g(r) = 1 ,
dla r > RP mamy g(r) = 0 .
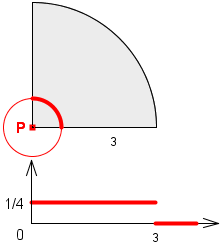
Czasami można od razu narysować funkcję gęstości.
Ta obok przyjmuje tylko dwie wartości: 0 i 1/4.
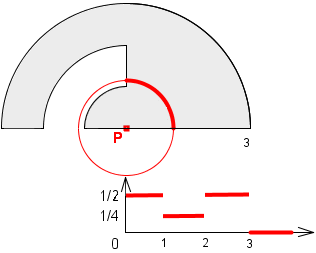
A ta trzy: 0, 1/4 i 1/2.
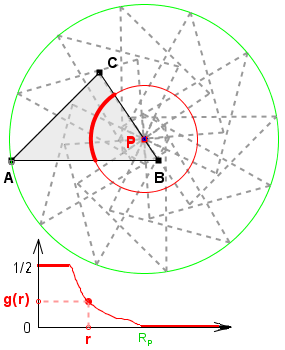
Gdy pinezkę wbijemy w bok wielokąta (ale nie w wierzchołek),
to gęstość w pobliżu 0 jest równa 1/2.
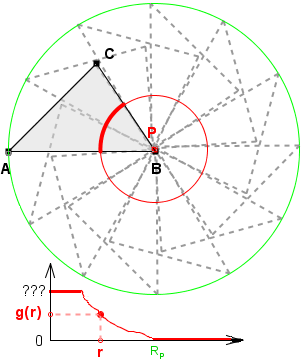
Gdy pinezkę wbijemy w wierzchołek wielokąta, to gęstość w pobliżu 0 jest stała, jaka?
Dla pinezki urojonej, gęstość w pobliżu 0 jest równa 0.
Przejdziemy teraz do wyznaczania wzorów funkcji gęstości.
Niestety nawet dla trójkąta równobocznego wymagają one znajomości
trygonometrii i funkcji odwrotnych do funkcji trygonometrycznych.
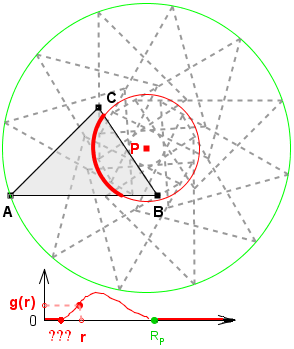
Niech trójkąt ABC ma bok długości 3 i niech pinezka P będzie wbita w środek okręgu wpisanego (i opisanego) na tym trójkącie.
Oczywiście rP =
![]() /2 oraz RP =
/2 oraz RP = ![]() .
.
Dla r takich, że rP < r < RP
gęstość g(r) = 6![]() / 2
/ 2![]() .
.
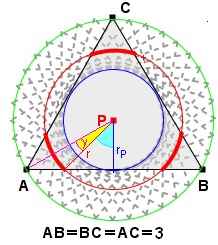
Dalej trzeba tylko(?) wyznaczyć kąt
![]() ,
w czym pomocny jest rysunek obok:
,
w czym pomocny jest rysunek obok:
![]() = 2
= 2![]() /6 - arccos( rP/r).
/6 - arccos( rP/r).
Ostatecznie po uproszczeniu mamy:
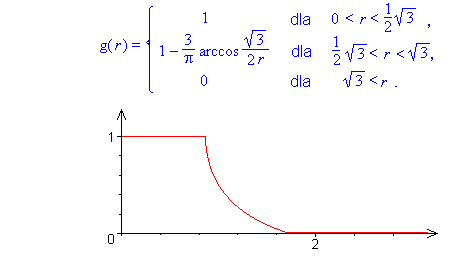
(Wykres pochodzi z programu komputerowego MAPLE.)
Zakończymy kilkoma trudniejszymi zadaniami.
ZADANIE 1.
Wyznacz wzór na gęstość wiatraczka zbudowanego z n-kąta foremnego z pinezką wbitą w środek okręgu opisanego.
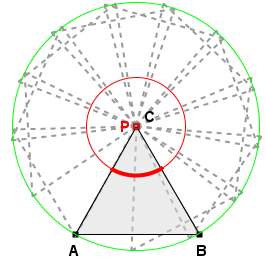
ZADANIE 2.
Wyznacz wzór na gęstość wiatraczka zbudowanego z trójkąta równobocznego z pinezką wbitą w wierzchołek.
ZADANIE 3.
Wyznacz funkcję gęstości dla wiatraczka zbudowanego z koła o promieniu R i pinezki odległej o d od środka koła.
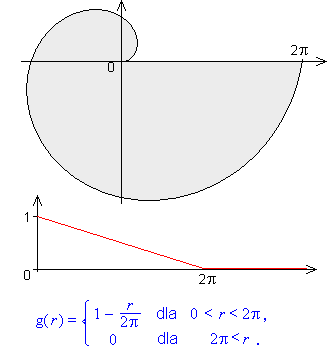
ZADANIE 4.
Sprawdź, że dla obszaru ograniczonego fragmentem spirali Archimedesa gęstość ma wykres taki, jak na rysunku obok.
ZADANIE 5.
Znajdź warunki, przy których funkcja gęstości jest nierosnąca.
ZADANIE 6.
Niech wiatraczek będzie zbudowany z figury f z wbitą pinezką P.
Porównaj funkcję gęstości g(r) z funkcjami
g1(r), g2(r) i g3(r)
określonymi poniższymi wzorami:
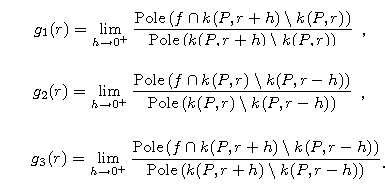




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
