Poniższy wigwam typu "bramka" o szerokości 2R i wysokości H ma stelaż-siatkę zbudowaną z odcinków, których końce dzielą poprzeczkę AB i łuk półokręgu w tym samym stosunku. W szczególności, gdy P jest środkiem AB, to Q jest środkiem łuku CD. Ogólnie:
COQ / QOD .Powyższa reguła będzie obowiązywała stale, choć zmieniać będziemy odcinek AB i łuk CD. Interesować nas będzie powierzchnia siatki i objętość wigwamu, czyli bryły tą siatką ograniczonej (o podstawie będącej częścią koła).
Można przesuwać suwaki i punkty O, P.
Najpierw zajmiemy się prostymi wigwamami.
Na początek niech punkt A pokrywa się ze środkiem O podstawy i niech odcinek AB będzie prostopadły do podstawy. Ten wigwam ma trójkątne wejście ABD (niezależnie od kąta a).
Jaka jest jego objętość V?
Można przesuwać suwaki i punkty O, P.
ROZUMOWANIE
Zobacz przekroje PQO tej bryły. Gdy na odcinku AB wybierzemy punkty Pk dzielące go na n równych części, to odpowiadające im punkty Qk podzielą łuk CD na jednakowe części, więc odcinki OQk podzielą podstawę na n jednakowych wycinków.
Cały wigwam jest teraz podzielony na n sektorów.
Sektory wyglądają (niemal) jak ostrosłupy o jednakowych podstawach.
Różnią się jedynie wysokościami.
Punkty Pk i Pn–k leżą symetrycznie względem punktu S - środka odcinka AB. Zatem suma objętości sektorów odpowiadających punktom Pk i Pn–k jest równa dwukrotności objętości sektora odpowiadającego punktowi S.
Objętość V całego wigwamu jest równa sumie objętości par sektorów, więc wynosi
n × objętość sektora odpowiadającego punktowi S, czyli dostajemy
WZÓR
Uwaga 1. Powyższe rozumowanie tylko w jednym miejscu nie jest precyzyjne, gdy mówimy, że sektory są niemal ostrosłupami. Można to sprecyzować, szacując z góry i z dołu objętość sektora objętościami ostrosłupów o wierzchołkach Pk i Pk+1.
Dlaczego nie podaliśmy wzoru na objętość za pomocą jakichś znaczków, tylko słowami?
Poniżej zobaczymy, że takie sformułowanie jest wygodniejsze i bardziej uniwersalne.
Sprawdź, że zarówno wzór na objętość jak i całe rozumowanie są poprawne w przypadku, gdy podstawą wigwamu jest:
- pełne koło ( a = 360 ),
- ćwiartka koła ( a = 90 ),
- dowolny wycinek koła ( 0 < a < 360 ).
Sprawdź, że zarówno wzór na objętość jak i całe rozumowanie są poprawne w przypadku, gdy punkty A, B leżą na prostopadłej do podstawy przechodzącej przez punkt O.
Można przesuwać suwaki i punkty O, P, A.
Sprawdź, że zarówno wzór na objętość jak i całe rozumowanie są poprawne w przypadku, gdy punkty A, B, O są współliniowe.
Można przesuwać suwaki i punkty O, P, A.
Gdy punkty A, B, O nie są współliniowe, objętość jest większa niż ta podana we wzorze.
Pokażemy to na szczególnym przykładzie wigwamu o podstawie będącej półkolem, gdy ABDC jest prostokątem prostopadłym do podstawy.
Można przesuwać suwaki i punkt O.
Podział odcinka AB na n jednakowych części wyznacza
podział wigwamu na n sektorów.
Przyjrzyjmy się k-temu sektorowi OPP'QQ'
(tu i dalej nie piszemy indeksu k przy tych punktach).
Dzielimy go na dwa czworościany: OQQ'P' i OPP'Q. Mamy
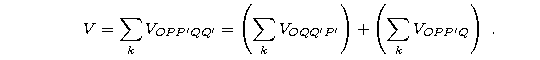
Łatwo obliczamy pierwszą sumę:
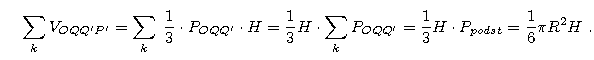
Druga jest równa:
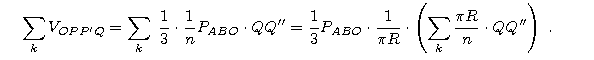
Suma w nawiasie jest powierzchnią boczną klina, o czym pisaliśmy już w tekście
Klina klinem, i jest równa 2R 2. Stąd
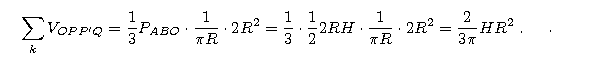
Zatem
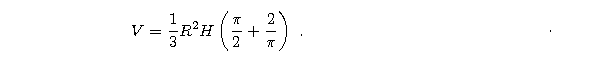
Jak skomplikowane mogą być wigwamy? Zobacz.
Można przesuwać suwaki i punkt O.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
