Poniższa bryła ma dwie ściany trójkątne, jedną prostokątną i jedną 'wypaczoną' w-ścianę czworokątną ABC'A'. Taka bryła powstała z graniastosłupa ABCA'B'C', który specjalną piłą-wyrzynarką podzielono na dwie części. Ostrze piły, odcinek PP', prowadzono tak, aby końce P i P' w jednakowym czasie przebyły odcinki AB i A'C', tzn. aby w każdej chwili dzieliły te odcinki w tym samym stosunku:
Można przesuwać suwaki i punkty A, P, Q.
Czerwone odcinki nie są równoległe, ale oba są równoległe do płaszczyzny BCC' (zobacz je 'z góry').
Środki (wszystkich) czerwonych odcinków tworzą odcinek o końcach będących środkami krawędzi AA' i BC'.
Ogólnie punkty czerwonych odcinków dzielące je w ustalonym stosunku tworzą odcinek o końcach dzielących krawędzie AA' i BC' w tym samym stosunku.
Wynika to z uogólnienia twierdzenia 1a,
z tekstu Równoległościan? Może tak, może nie....
Zatem w-ściana ABC'A' mogła powstać również z cięcia graniastosłupa odcinkami łączącymi krawędzie AA' i BC'.
Nie każdy przekrój w-ściany ABC'A' jest odcinkiem. Gdy przetniemy tę w-ścianę płaszczyzną równoległą do ABB'A', to dostaniemy fragment hiperboli.
Zadanie 0. W-ścianę nazywa się często siodłem. Jak myślisz, dlaczego?
Zadanie 1. Jakie równanie spełniają współrzędne punktów w-ściany ABC'A', gdy C'=(4,4,4)?
Wskazówka. Pomyśl o punktach o ustalonej współrzędnej x.
Graniastosłup jest podzielony w-ścianą ABC'A' na dwie bryły o jednakowej objętości.
Widać to, gdy potniemy graniastosłup 'na cienkie plasterki' płaszczyznami równoległymi do BCC' (na rysunku widać jeden taki 'plasterek').
Można przesuwać suwaki i punkty A, P, Q, R.
Gdy mamy cztery punkty A, B, C, D (nie leżące w jednej płaszczyźnie), to przez w-ścianę ABCD rozumiemy powierzchnię wyznaczoną przez wszystkie odcinki PP' o końcach dzielących odcinki AB i DC w tym samym stosunku: AP / PB = DP' / P'C.
Zauważ, że w-ściana DABC jest tą samą w-ścianą co ABCD.
Twierdzenie 1
Czworościan ABCD jest podzielony w-ścianą ABCD na dwie bryły o jednakowej objętości.
Dowód zobaczysz, 'plasterkując' czworościan płaszczyznami równoległymi jednocześnie do krawędzi BC i AD (przesuń suwak [przekrój P]).
Można przesuwać suwaki i punkty A, P.
Zadanie 2. Ostrosłup prawidłowy ABCDW ma wysokość WW' = 7 i krawędź AB = 4. Jaki jest stosunek objętości brył powstałych z tego ostrosłupa po rozcięciu:
a) w-ścianą ABCW?
b) w-ścianą ACWD?
Zadanie 3. Sześcian ABCDA'B'C'D' ma krawędzie długości 4. Jaki jest stosunek objętości brył powstałych z tego sześcianu po rozcięciu:
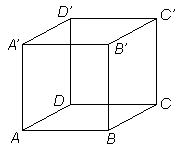a) w-ścianą ABB'D'?
b) w-ścianą ABCD'?
c) w-ścianą ACB'D'?
d*) w-ścianą ABCA'?
Zadanie 4. Wyznacz objętość czworo-w-ścianu przedstawionego na rysunku, gdy AA' = H, wierzchoki B, C, D, E leżą w płaszczyźnie symetrii odcinka AA' i tworzą kwadrat o przekątnej 2r i o środku w środku odcinka AA'.
Można przesuwać suwaki i punkt A.
Z w-ścian można zbudować trój-w-ścian. Zadziwiające? Zobacz.
Zadanie 5.
Wyznacz objętość trój-w-ścianu przedstawionego na rysunku,
gdy A = (0, 0, 0), B' = (a, 0, 0), B'' = (0, 0, a), C' = (a, a, a),
C'' = (a, -a, a).
Można przesuwać suwaki i 'wypełnione' punkty.
Zadanie 6*. Wyznacz objętość trój-w-ścianu przedstawionego na rysunku, gdy AA' = H, wierzchołki B, C, D, leżą w płaszczyźnie symetrii odcinka AA' i tworzą trójkąt równoboczny o środku w środku odcinka AA' i o wysokości 1,5r.
Można przesuwać suwaki i punkt A.
Zadanie 7**.
Ile jest wszystkich w-ścian wyznaczonych przez wierzchołki sześcianu?
Wszystkie te w-ściany (na raz) dzielą sześcian na wiele brył. Na ile?
Ile jest wśród nich par brył przystających?
Jakie są objętości tych brył?
