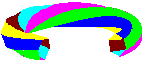
Poprzednio (patrz Zakręcone graniastosłupy (1)) budowaliśmy graniastorusy wyginając odpowiednio graniastosłupy i sklejając ich podstawy.
Teraz zakręcimy i dodatkowo pokręcimy. Ojoj, co z tego wyjdzie?
Skręcamy długi graniastosłup o podstawie kwadratowej i sklejamy:

4.0) |
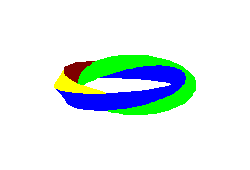
4.4) |
W obu przypadkach dostajemy powierzchnię "czterościenną".
Skręcamy długi graniastosłup o podstawie trójkątnej i sklejamy:

3.0) |
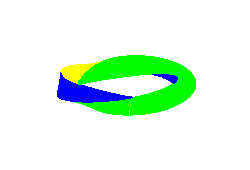
3.3) |
W obu przypadkach dostajemy powierzchnię "trójścienną".
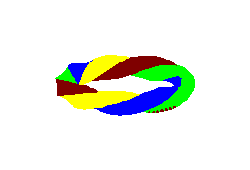
4.8) |
Również teraz dostajemy powierzchnię "czterościenną".

3.1) |

3.2) |
A teraz dostaliśmy powierzchnię "jednościenną": żółto-zielono-niebieską.
Czym poniższa różni się od powyższych?

?.?) |
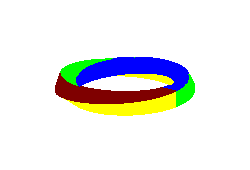
4.2) |
A teraz dostaliśmy powierzchnię "dwuścienną": żółto-zieloną i brązowo-niebieską.
A jakie powierzchnie dostaniemy skręcając długi graniastosłup o podstawie będącej 24-kątem foremnym i sklejając go na różne sposoby? "Iluścienne" ?
Czy więcej rodzajów powierzchni dostaniemy skręcając długi graniastosłup o podstawie będącej 25-kątem foremnym i sklejając go na różne sposoby?

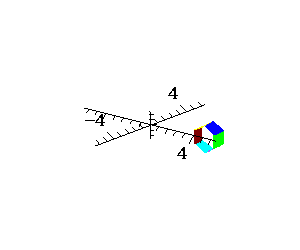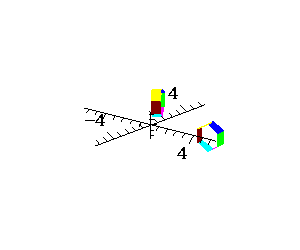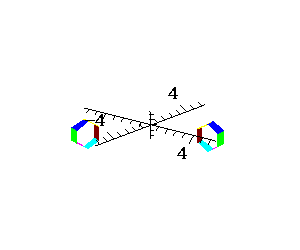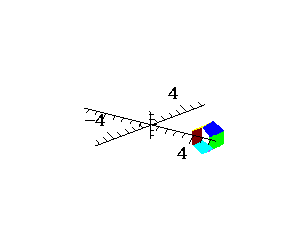







Pomysł Calatravy
Moskwa ma swój
Podobny wieżowiec, choć może nie z takim rozmachem zbudowany, jest w Moskwie.
To Wieża "Ewolucja" zaprojektowana przez brytyjskiego architekta Tony'ego Kettle we współpracy z profesor sztuki Uniwersytetu w Edynburgu - Karen Forbes. 55-piętrowy budynek (Краснопресненская наб. 2-3) jest częścią Moskiewskiego Międzynarodowego Centrum Biznesowego, ma wysokość 246 m (XII miejsce pod względem wysokości w Rosji i XX w Europie) i powierzchnię użytkową 169 000 m2. Wieżowiec wybudowano w latach 2007-2011-2014. Mieści się w nim m.in. Urząd Stanu Cywilnego (co podobno było powodem, że projektant zainspirował się rzeżbą Rodina Pocałunek). Na najwyższym piętrze jest sala balowa o powierzchni 2000 m2. Każde piętro budynku obrócone jest o 3° w stosunku do poprzedniego, a łączny obrót ostatniego piętra w stosunku do pierwszego wynosi 135°.