Okręgi dopisane trójkąta prostokątnego

Trójkąt jest jedną z najciekawszych figur w geometrii. Chociaż składa się zaledwie z trzech odcinków, to liczba jego własności jest ogromna. Podobnie prostą a jednocześnie ciekawą figurą jest okrąg. W tym artykule zbadamy kilka intrygujących własności okręgów dopisanych do trójkąta prostokątnego.

Definicja. Okręgiem dopisanym do trójkąta nazywamy okrąg styczny do boku tego trójkąta i do przedłużeń dwóch pozostałych boków.

Każdy trójkąt posiada jeden okrąg wpisany i trzy okręgi dopisane - patrz rysunek.

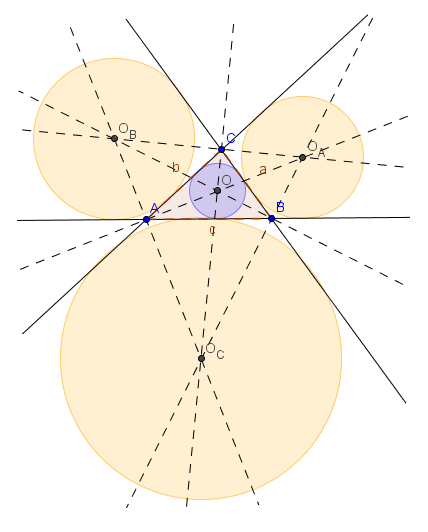
Środek O okręgu wpisanego w trójkąt leży w przecięciu dwusiecznych jego kątów wewnętrznych.

Środki O_a, O_b i O_c okręgów dopisanych do trójkąta leżą w przecięciu dwusiecznej odpowiedniego kąta wewnętrznego i dwusiecznych pozostałych kątów zewnętrznych trójkąta.
Przypomnijmy, że kąty zewnętrzne wielokąta są przyległe do jego kątów wewnętrznych.

Udowodnimy teraz kilka ciekawych własności okręgów dopisanych do trójkąta prostokątnego. Wprowadźmy oznaczenia:

• a i b to przyprostpokątne, a c - przeciwprostokątna,
• r to promień okręgu wpisanego w trójkąt, a r_a, r_b, r_c  - promienie okręgów dopisanych, stycznych do odpowiednich boków trójkąta.

Własność 1

Zachodzi zależność  r + r_a + r_b = r_c.

Zadanie to pojawiło się na I etapie III Olimpiady Matematycznej w roku 1951.

Dowód algebraiczny

Można łatwo pokazać, że 
[tex] \; r=\frac{P}{p}, \quad {r}_{a}=\frac{P}{p-a}, \quad {r}_{b}=\frac{P}{p-b}, \quad {r}_{c}=\frac{P}{p-c} [/tex],
gdzie P to pole trójkąta ABC, a p jest połową jego obwodu, czyli [tex] p=\frac{a+b+c}{2}[/tex].

Dowody tych zależności można znaleźć m.in. w Miniaturach Matematycznych nr 47 wydawnictwa Aksjomat z Torunia. 

Ponadto wiemy, że trójkąt jest prostokątny, zatem zachodzi a²+b² = c². Stąd otrzymujemy:

[tex]r+{r}_{a}+{r}_{b}-{r}_{c}=\frac{P}{p} + \frac{P}{p-a} + \frac{P}{p-b} - \frac{P}{p-c} = {P} \left(\frac{1}{p} + \frac{1}{p-a} + \frac{1}{p-b} - \frac{1}{p-c}\right)=[/tex]

[tex]=P \left(\frac{2p-a}{p(p-a)} + \frac{b-c}{(p-b)(p-c)} \right) = P \left(\frac{b+c}{p(p-a)} +\frac{b-c}{(p-b)(p-c)} \right)=[/tex]

[tex]=P \frac{b(p-b)(p-c)+c(p-b)(p-c)+bp(p-a)-cp(p-a)}{p(p-a)(p-b)(p-c)}[/tex].

Wykorzystamy teraz wzór Herona [tex]P=\sqrt{p(p-a)(p-b)(p-c)}[/tex], podstawiając go w mianowniku ostatnio otrzymanego wyrażenia.

[tex]P \frac{b(p^2-p(b+c)+bc+p^2-ap)+c(p^2-p(b+c)+bc-p^2+ap)}{P^2}=[/tex]

[tex]= \frac{b(2p^2-p(a+b+c)+bc)+c(p(a-(b+c) )+bc)}{P} =[/tex]

[tex]= \frac{b(2p^2-p \cdot 2p+bc)+c(p(a-(b+c) )+bc)}{P} =[/tex] 

[tex]= \frac{b^2 c+c \left( \frac{(a+b+c)}{2} \cdot (a-(b+c))+bc \right)}{P} =\frac{c}{P} \cdot \left( b^2+ \frac{a^2 -{(b+c)}^{2}}{2}+bc \right)=[/tex]

[tex]= \frac{c}{P} \cdot \left( \frac{2b^2+a^2-b^2-2bc-c^2+2bc}{2} \right)= [/tex]

[tex]= \frac{c}{P} \cdot \left( \frac{(a^2+b^2 )-c^2}{2} \right) = \frac{c}{P} \cdot \left( \frac{c^2-c^2}{2} \right) = 0 [/tex],

co kończy dowód.

Dowód geometryczny

Narysujmy trójkąt prostokątny wraz z okręgiem dopisanym do boku c oraz okrąg, na którym leżą (jako trzy punkty niewspółliniowe) środki okręgów dopisanych O_a,O_b i O_c (patrz rysunek). Środek tego okręgu oznaczmy przez S, a jego promień przez R. Punkty D, E, F i G są rzutami prostokątnymi odpowiednio punktów O, O_a, O_b i O_c na prostą AC.

Poprowadźmy teraz prostą równoległą do AC przechodzącą przez punkt S. W ten sposób wyznaczymy średnicę O_aH okręgu o środku w S. Stąd widać, że R = r_a + r_b.

Niech |∢CBA| = 2α i |∢CAB| = 2β. Wtedy |∢CBO| = |∢ABO| = α oraz |∢CAO| = |∢BAO| = β, ponieważ proste przechodzące odpowiednio przez punkty B, O oraz A, O są dwusiecznymi kątów CBA i CAB. Wobec tego α + β = 45°. Ponadto |OD| = |OJ| = |OK| = r.
 

Zauważmy ponadto, że |∢CAO|=|∢JOO_a|, gdyż są to kąty odpowiadające oraz |∢CAO|=|∢OO_aM|, ponieważ są to kąty naprzemianległe. Rozwartość kąta BOO_a obliczymy w następujący sposób:
2(90°-β)+90°+β+90°-α+|∢BOO_a|=360°, skąd otrzymujemy |∢BOOa| = α+β=45°. Łatwo zauważyć, że trójkąt SO_aO_c jest równoramienny (bo odcinki SO_a i SO_c są promieniami okręgu o środku w S), a z tego wynika, że |∢SO_aO_c|=|∢SO_cO_a| = α (patrz rysunek). Wobec tego |∢OO_aO_c| = α+β = 45°, więc trójkąt OO_aB jest prostokątny i równoramienny. Zatem trójkąty MO_aB i KBO są przystające, co implikuje |MB| = |OK| = r.

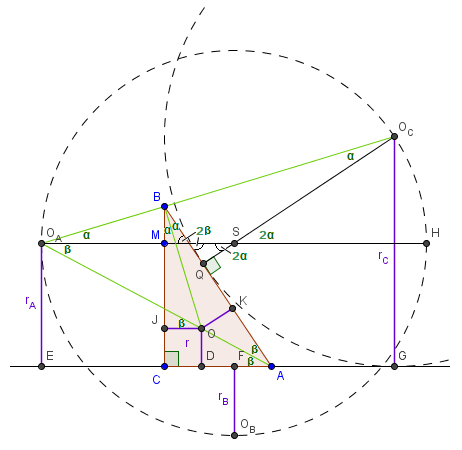
Niech N będzie teraz punktem przecięcia odcinków BQ i MS. Dodatkowo otrzymujemy, że trójkąty BNM i SQN są przystające (dowód tego faktu pozostawiamy czytelnikowi). Zatem |BM| = |SQ| = r, a więc możemy zapisać, że r_c = R+r, skąd wyznaczając R, otrzymujemy R = r_c-r. Porównując oba otrzymane wyniki, dostajemy r_a+r_b = r_c-r, co daje tezę.  

Własność 2

Zachodzą zależności:  r_a = a – r      r_b = b – r      r_c = c + r.

Dowód

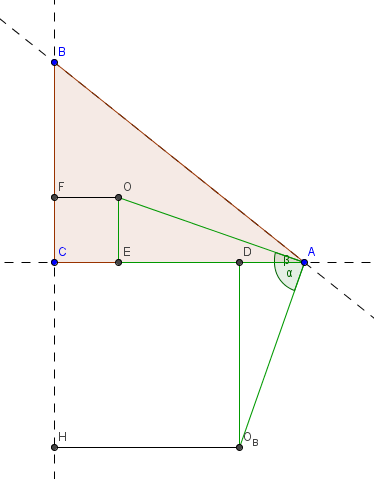
Wniosek 1

Promienie okręgów dopisanych i okręgu wpisanego w trójkąt prostokątny można prosto wyrazić za pomocą długości boków trójkąta (p oznacza połowę obwodu trójkąta).

r_a = p – b      r_b = p – a      r_c = p      r = p – c. 

Definicja. Nazwijmy okręgiem nadpisanym trójkąta ABC okrąg opisany na trójkącie OaObOc rozpiętym na środkach okręgów dopisanych trójkąta ABC.

Wniosek 2

Promień R okręgu nadpisanego dowolnego trójkąta prostokątnego jest równy długości przeciwprostokątnej tego trójkąta, tzn. R=c. Pozwala to w łatwy sposób skonstruować okrąg nadpisany, wyznaczając tylko dwa środki okręgów dopisanych do trójkąta.

Zachęcamy czytelników do samodzielnego poszukiwania dalszych własności okręgów dopisanych do trójkąta. Jest to dobra okazja do rozwijania swoich umiejętności matematycznych.