Jednym z najwcześniej opisanych fraktali (i to znacznie wcześniej niż powstał sam termin 'fraktal') był trójkąt Sierpińskiego (zwany też uszczelką Sierpińskiego). Konstrukcja tego zbioru była podana przez warszawskiego matematyka Wacława Sierpińskiego w 1915 roku.
Trójkąt Sierpińskiego otrzymuje się z trójkąta równobocznego, zaznaczając w jego wierzchołkach trójkąty równoboczne o 2 razy krótszym boku i usuwając czwarty pozostały na środku trójkąt równoboczny. Operację tę powtarza się w każdym z pozostałych trzech mniejszych trójkątów i tak w nieskończoność. Punkty pozostające po nieskończenie wielu powtórzeniach tej operacji tworzą trójkąt Sierpińskiego.
Piramidę Sierpińskiego otrzymuje się z czworościanu foremnego, zaznaczając w jego wierzchołkach czworościany foremne o 2 razy krótszej krawędzi i usuwając pozostały na środku ośmiościan foremny. Operację tę powtarza się w każdym z pozostałych czterech mniejszych czworościanów i tak w nieskończoność. Punkty pozostające po nieskończenie wielu powtórzeniach tej operacji tworzą piramidę Sierpińskiego.
Przygotujemy teraz bryłę, która może być prawdziwą ozdobą gabinetu matematycznego. Pojedyncze elementy wykonuje się łatwo i szybko. Ponieważ całość ma budowę modułową, a do jej wykonania potrzebnych jest dużo elementów (co najmniej 64), może być wspólnym dziełem większej grupy uczniów
Wykonanie modelu
Czworościany można sklejać, łącząc odpowiednie krawędzie po zewnętrznej stronie przezroczystą taśmą klejącą. Jest to metoda szybka i skuteczna, a spektakularny efekt końcowy można uzyskać w stosunkowo krótkim czasie.
Jeżeli bardziej zależy nam na trwałości i estetyce modelu, lepiej jest skorzystać z siatki ze "skrzydełkami" i kleić elementy zwykłym klejem szkolnym. Polecamy klej 'magic' (w czerwonej tubce) - jest elastyczny, bezbarwny i dobrze skleja papier. Czas pracy jest o wiele dłuższy, ale ostateczny efekt bardziej satysfakcjonujący.
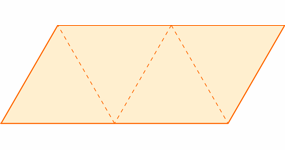
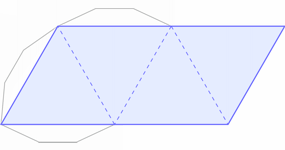
W zależności od sposobu klejenia, wybierz siatkę bez "skrzydełek" (diagram pomarańczowy) lub ze "skrzydełkami" (diagram niebieski). Klikając w wybrany diagram, pobierzesz plik w formacie pdf.
Łączenie poszczególnych etapów piramidy taśmą klejącą jest bardzo proste - wystarczy zetknąć odpowiednie skrajne wierzchołki dwóch brył i pociągnąć taśmą po ich wspólnej krawędzi.
Łączenie brył pośrednich sklejonych klejem jest nieco trudniejsze. Jeżeli mamy dobry klej, możemy zastosować klejenie stykowe i w miejscu połączenia wierzchołków wycisnąć go nieco więcej. Ułatwieniem w takim klejeniu może być bardzo delikatne przycięcie wierzchołka w doklejanym miejscu. Ten zabieg ma na celu zwiększenie powierzchni sklejenia, ale nie może zaburzyć kształtu piramidy, dlatego odcinamy jak najmniejszy kawałek.
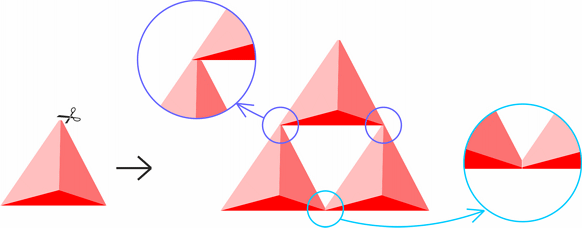
Oczywiście pomysłów na sklejanie małych czworościanów i łączenie kolejnych etapów piramidy może być znacznie więcej. Jeżeli mamy dobry klej i odpowiednio gruby papier, można np. sklejać stykowo krawędzie małych czworościanów, a do łączenia mniejszych piramid w większe używać dodatkowych usztywniających łączników. W poniższych modelach rolę takich łączników pełnią wykałaczki.
Poniżej prezentujemy gotowe modele piramidy Sierpińskiego IV stopnia. Piramidy wyższych stopni wymagają mocniejszych usztywnień w miejscach łączenia, np. patyczków od szaszłyków.
Modele III rzędu (zdj. 1) wykonali uczniowie, uczestnicy Zimowej Szkoły Matematyki. Nad każdym modelem pracowało 20 osób (w 4 grupach 5-osobowych, tworząc piramidy rzędu 2). Po 45- minutach piramidy były gotowe i można je było skleić do rzędu 3. Finalnego połączenia czterech części w piramidę rzędu IV (zdj. 2-4) dokonali studenci specjalności nauczycielskiej IM UWr (widoczni na zdj. 4).
Model wykonany przez autorkę artykułu.
