Wiadomo, że każdy trójkąt ma kilka środków, np. środek ciężkości M, środek okręgu opisanego O, środek okręgu wpisanego I, punkt przecięcia prostych zawierających wysokości (tzw. ortocentrum trójkąta H). Ale punktów szczególnych trójkąta jest znacznie więcej. Opowiemy o nich przy innej okazji. W tym artykule za punkty szczególne (oprócz wyżej wymienionych) uznamy jeszcze środki okręgów dopisanych do trójkąta.
Rozwiążemy teraz kilka zadań, które pozwolą nam lepiej poznać własności poszczególnych charakterystycznych punktów trójkąta.
Zad. 1. Wykaż, że jeśli dwa z punktów szczególnych trójkąta (oprócz środków okręgów dopisanych) pokrywają się, to trójkąt jest równoboczny. Rozważ sześć przypadków tego zadania.
Rozwiązanie. 1) H=O. Wówczas H1 = M1 i trójkąty AH1C oraz ABH1 są przystające (bkb), a stąd |AC| = |AB|. Analogicznie pokazujemy, że |AB| = |BC|. Stąd wynika teza.
2) H=M. Oba punkty leżą na prostych przechodzących przez A i prostopadłych do boku BC, zatem musi to być jedna prosta i stąd H1 = M1. Dalej jak przypadku 1).
3) H=I. Wówczas proste AH i AI się pokrywają, co oznacza, że wysokość AH1 jest dwusieczną kąta A, a stąd trójkąty AH1C i ABH1 sa przystające, czyli |AC| = |AB|. Analogicznie pokazujemy, że |AB|=|BC|. Stąd wynika teza.
4) O=M. Wówczas środkowa AM1 jest prostopadła do BC i M1=H1. Dalej jak w przypadku 1).
5) M=I. Wówczas środkowa AM1 jest jednocześnie dwusieczną kąta A. Środkowa dzieli pole trójkąta ABC na pół, a dwusieczna jest zbiorem punktów równoodległych od ramion AC i AB. Stąd wynika, że |AC| = |AB|. Analogicznie pokazujemy, że |AB| = |BC|. Z tego wynika teza.
6) I=O. Wówczas środki boków są jednocześnie punktami styczności okręgu wpisanego w trójkat, co oznacza, że trójkąty AOB, BOC i COA są przystające. Stąd wynika teza.
Zad. 2. Wykaż, że ortocentrum dzieli każdą wysokość na dwa odcinki o takich długościach, że ich iloczyn jest stały dla danego trójkąta.
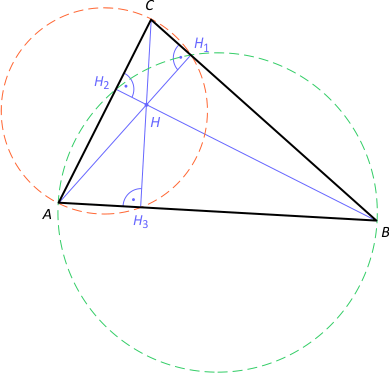
Rozwiązanie 1. Trójkąty AH3H i CH1H są podobne (kk). Zachodzi proporcja boków |AH|:|HH3| = |CH|:|HH1|, skąd |AH|·|HH1| = |CH|·|HH3|, co stanowi tezę. Analogicznie pokazujemy, że |AH|·|HH1| = |BH|·|HH2|.
Rozwiązanie 2. Zauważmy, że na czworokątach ABH1H2 i CAH3H1 można opisać okrąg (na mocy twierdzenia odwrotnego do twierdzenia o kątach wpisanych w okrąg opartych na tym samym łuku). Z twierdzenia o przecinających się cięciwach okręgu mamy |AH|·|HH1| = |BH|·|HH2| oraz |AH|·|HH1| = |CH|·|HH3|, skąd |AH|·|HH1| = |BH|·|HH2| = |CH|·|HH3|, c.n.d.
Zad. 3. Wykaż, że punkty symetryczne do ortocentrum względem boków trójkąta leżą na okręgu opisanym na tym trójkącie.
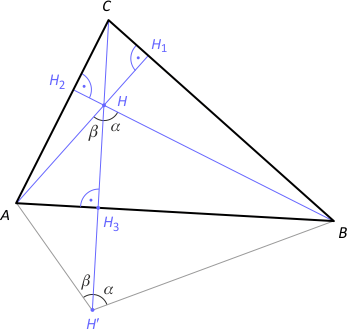
Rozwiązanie. Niech H' oznacza punkt symetryczny do ortocentrum H względem boku AB. Zauważmy, że |∡AH'B| = |∡AHB| = |∡AHH3|+|∡H3HB| = 90°–|∡HAH3|+90°–|∡HBH3| = 90°–|∡H1AB|+90°–|∡H2BA| = 90°–(90°–β)+90°–(90°–α) = α+β = 180°–γ = 180°–|∡ACB|, co oznacza, że na czworokącie AH'BC można opisać okrąg. Stąd wynika teza. Pozostałe przypadki rozpatrujemy analogicznie.
Zad. 4. Przez środek E wysokości AH1 w trójkącie ABC i wierzchołek C poprowadzono prostą przecinającą AB w punkcie D. Wiedząc, że |AE| = √(|EC|∙|ED|) wykaż, że E pokrywa się z ortocentrum trójkąta.
Rozwiązanie. Skoro |AE| = √(|EC|∙|ED|), to |AE|2 = |EC|·|ED|, a to oznacza, że |AE|·|EH1| = |EC|·|ED|, czyli |AE|:|ED| = |EC|:|EH1|. To oznacza, że trójkąty AED i CEH1 są podobne (z cechy bkb). Stąd |∡ADE| = 90°.
Zad. 5. Znajdź punkt X taki, że PBXM1 = PCXM1 = PCXM2 = PAXM2 = PAXM3 = PBXM3 oraz punkt Y taki, że PBYC = PAYC = PAYB.
Rozwiązanie. Rozważmy środek ciężkości M trójkąta ABC, czyli punkt przecięcia środkowych tego trójkąta. Każda środkowa dzieli pole trójkąta na pół. Stąd PCAM3 = PCM3B, a P1 = PAMM3 = PBMM3, P2 = PBMM1 = PCMM1 oraz P3 = PCXM2 = PAMM2. Stąd mamy 2P3 + P1 = 2P2 + P1, czyli P2= P3. Analogicznie P1=P2. Zatem szukanym punktem X (a także Y) jest środek ciężkości M.
Zad. 6. Wykaż, że w trójkącie ABC (o bokach długości a, b, c) promień okręgu opisanego ma długość 1/6(ab+bc+ac):(d1+d2+d3), gdzie di oznacza odległość środka ciężkości trójkąta od poszczególnych boków.
Rozwiązanie. Na mocy poprzedniego zadania mamy 1/2·ad1 = 1/2·bd2 = 1/2·cd3 = 1/3·P. Stąd d1=2P/3a, d2 = 2P/3b i d3 = 2P/3c, zatem d1+d2+d3 = 2/3P(1/a + 1/b + 1/c), co po rozszerzeniu ułamków w ostatnim nawiasie przez abc jest równe 2/3P(bc+ac+ba)/abc, czyli (d1+d2+d3):(ab+ac+bc) = 2/3P/abc. Pamiętając, że P = abc/4R, otrzymujemy (d1+d2+d3):(ab+ac+bc) = 1/6R, a stąd R = 1/6·(ab+bc+ac)/(d1+d2+d3), c.n.d.
Zad. 7. Wykaż, że w trójkącie ABC kąty HAB i OAC mają równe miary, gdzie H - ortocentrum, O - środek okręgu opisanego na tym trójkącie.
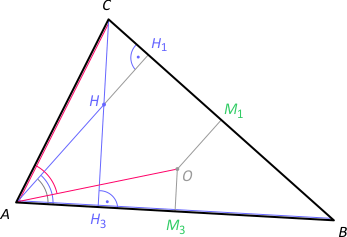
Rozwiązanie. Zauważmy, że |∡HAB| = |∡H1AB| = 90°–β. Z drugiej strony w trójkącie równoramiennym AOC kąt środkowy AOC ma miarę 2β. Stąd |∡OAC| = 1/2·(180°–2β) = 90°–β, c.n.d. To rozwiązanie zakłada, że trójkąt ABC jest ostrokątny (środek okręgu opisanego leży wewnątrz trójkąta). Dla innych trójkątów rozumowanie jest analogiczne. Proponujemy dowód przeprowadzić samodzielnie.
Zad. 8. Wykaż, że jeśli kąt w wierzchołku A trójkąta ABC ma 60°, to |AH| = R, gdzie H - ortocentrum, R - promień okręgu opisanego na trójkącie.
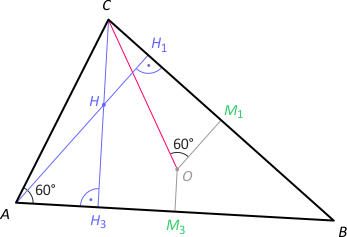
Rozwiązanie. Kąt środkowy COB ma miarę 120°, a stąd |∡COM1| = 60°, zatem trójkąt OM1C jest trójkątem ekierkowym, w którym |OM1| = |OC|/2 = R/2. Trójkąty AHC i OM1M3 są podobne z cechy kkk, bo mają boki parami równoległe (dlaczego?). Skala tego podobieństwa wynosi 2 (dlaczego?). Ponieważ w tym podobieństwie odpowiadającymi bokami są AH i OM1, zachodzi |AH| = 2|OM1| = R. To rozwiązanie zakłada, że trójkąt ABC jest ostrokątny (środek
okręgu opisanego leży wewnątrz trójkąta). Dla innych trójkątów
rozumowanie jest analogiczne. Proponujemy dowód przeprowadzić
samodzielnie.
Zad. 9. Wykaż, że jeśli jeden z kątów trójkąta ma miarę 60°, to |OI| = |IH|, gdzie H - ortocentrum, O - środek okręgu opisanego na trójkącie, I – środek okręgu wpisanego w trójkąt (tzw. incentrum trójkąta).
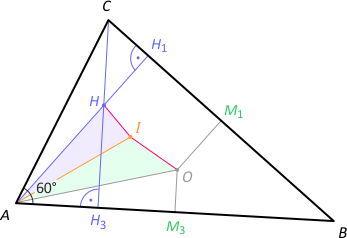
Rozwiązanie. Niech |∡A| = 60°. Na mocy zad. 8 mamy |AH| = R. Zauważmy, że |∡CAH| = |∡CAH1| = 90°–γ = |∡M3AO|, bo kąt środkowy AOB ma miarę 2γ (równość |∡CAH| = |∡M3AO| wynika też od razu z zad, 7). Wobec tego oraz faktu, że AI jest dwusieczną kąta A, kąty HAI i IAO mają równe miary. Na mocy cechy bkb trójkąty AHI oraz AIO są przystające, a stąd wynika teza. To rozwiązanie zakłada, że trójkąt ABC jest ostrokątny (środek
okręgu opisanego leży wewnątrz trójkąta). Dla innych trójkątów
rozumowanie jest analogiczne. Proponujemy dowód przeprowadzić
samodzielnie.
Zad. 10. Wykaż, że jeśli w trójkącie ostrokątnym ABC kąt w wierzchołku A ma miarę 60°, to punkty B, C, O, H, I oraz Ia leżą na jednym okręgu (Ia to środek okręgu dopisanego do trójkąta, stycznego do boku przeciwległego do wierzchołka A).
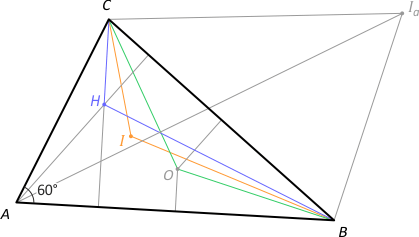
Rozwiązanie. Zauważmy, że |∡CIaB| = 180°–(90°–γ/2) – (90°–β/2) = γ/2 + β/2 = 90°–α/2 = 60°. Z kolei |∡CIB| = 90°+α/2 = 120° (bo to kąt między dwusiecznymi), |∡COB| = 120° (bo to kąt środkowy) oraz |∡CHB| = 180°–|∡H2HC| = 180°–(90°–(90°–60°) = 120°. Zatem czworokąty CIBIa, COBIa oraz CHBIa są wpisane w okrąg opisany na trójkącie CBIa, a stąd wynika teza.
