Zegarowe opowieści

Wiele zadań na różnych konkursach matematycznych (i to zarówno dla szkół podstawowych jak i dla starszych kategorii wiekowych) dotyczy mierzenia czasu i własności zegarów (wskazówkowych lub z wyświetlaczem cyfrowym). Dlatego warto nabyć wprawy w rozwiązywaniu takich zadań. Zebrane tu zadania i łamigłówki pochodzą głównie z różnych edycji Międzynarodowych Mistrzostw w Grach Matematycznych i Logicznych. W obrębie działu tematycznego są ułożone ze względu na rosnący stopień trudności, co powinno ułatwić ich rozwiązywanie i wykorzystanie do zajęć na kółku matematycznym.

Zachęcamy do dopisywania w komentarzach kolejnych ciekawych zadań na ten temat, podawania linków do takich zadań lub dzielenia się ich rozwiązaniami.

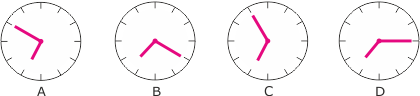
Zadanie 1. Z czterech zegarów oznaczonych literami A, B, C, D (patrz rysunek) jeden wskazuje dokładny czas, jeden śpieszy o 20 minut, drugi o 25, a jeden późni o 5 minut. Który zegar wskazuje dokładny czas?

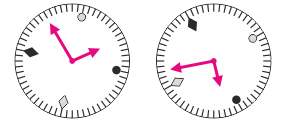Zadanie 2. Dwa jednakowe zegary (patrz rysunek) zatrzymały się ostatniej nocy. Rano zdjęto je ze ściany do nastawienia. Wiadomo, że pierwszy stanął o 1:53. O której godzinie zatrzymał się drugi zegar?

Zadanie 3. Pan Jarek ma zegarek bez cyfr na tarczy, którego wskazówki obracają się w przeciwnym kierunku niż normalnie. Półtorej godziny po północy pan Jarek spojrzał na odbicie tarczy swojego zegarka w lustrze. Którą godzinę zobaczył? Która godzinę zobaczyłby patrząc wprost na tarczę?

Zadanie 4. Aneta przygotowuje się do wyjścia na wieczorne spotkanie. Staje przed lustrem i widzi w nim odbicie zegarka. - O rany! O tej godzinie powinnam już wyjść, a jeszcze nie jestem gotowa! – myśli. Wtedy spogląda przez okno na zegar na wieży kościelnej i stwierdza z ulgą, że ma jeszcze godzinę na przygotowanie się. Która jest godzina?

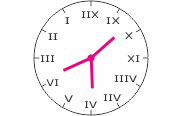
Zadanie 5. To lustrzane odbicie zegara (patrz rysunek), w którym wszystkie wskazówki mają tę samą długość. Ostatnią pełną godzinę zegar pokazywał 1111 sekund temu. Którą pokazuje teraz?

Zadanie 6. Jaki kąt tworzą wskazówki zegara o 20:06?

Zadanie 7. Pewnego słonecznego przedpołudnia Beata spojrzała na zegarek i zauważyła, że jego wskazówki tworzą linię prostą. Linia ta podzieliła liczby na tarczy na dwie części o równych sumach. Która była godzina?

Zadanie 8. W siedzibie Klubu Miłośników Gier Logicznych znajduje się zabytkowy zegar, który ma trzy wskazówki: sekundową, minutową i godzinową. Każda porusza się skokowo (sekundowa co sekundę, minutowa co minutę, a godzinowa co 12 minut) i może zajmować jedną z 60 pozycji. O 12:00 wskazówki pokrywają się. Na czas remontu zegara oryginalne wskazówki zostały zastąpione trzema jednakowymi, a tarcza została przypadkowo obrócona i nie wiadomo, gdzie jest godzina12. Jednak zegar cały czas prawidłowo chodzi. Pewnego popołudnia prezes Klubu spojrzał na zegar (patrz rysunek) i zauważył, że wskazówki zegara utworzyły literę T. Po niecałych 30 minutach spojrzał ponownie i spostrzegł, że wskazówki tworzą literę Y i kąty 120°. Która była godzina w chwili, gdy prezes pierwszy raz spojrzał na zegar?

Zadanie 9. Zegarmistrz przez pomyłkę wstawił do zegarka wskazówkę godzinową identyczną z minutową. Ile jest takich położeń wskazówek w ciągu doby, przy których nie można jednoznacznie odczytać czasu?

Zadanie 10. Trzy mrówki znajdują się na zegarze: jedna z nich śpi na środku tarczy, druga na końcu małej wskazówki, a trzecia na końcu dużej, mającej 22 cm długości. Trzecia mrówka obudziła się, gdy zegar wybijał 15:00, i skierowała się ze stałą prędkością po wskazówce do środka tarczy, co zajęło jej godzinę. W tym czasie mrówki raz tworzyły trójkąt równoboczny. Jaka jest długość małej wskazówki?

Zadanie 11. Mój kolega ma zegarek, który funkcjonuje w dziwny sposób: wskazówka sekundowa obraca się w odwrotnym kierunku niż minutowa i godzinowa, które obracają się normalnie. O godzinie 14:00 i 14:45 zegarek kolegi wskazywał dokładny czas. Ile razy to się jeszcze zdarzyło pomiędzy tymi godzinami?

Zadanie 12. Albert eksperymentuje z zegarkami własnej konstrukcji. Każdy z nich ma 24-godzinny cyferblat, pierwszy zegar chodzi w normalnym tempie, ale w odwrotnym kierunku, a drugi w normalnym kierunku, ale dwa razy szybciej. O 13:00 oba zegary wskazywały dokładny czas. O której godzinie wskazówki na tarczach obu zegarów będą znowu w zgodnym położeniu?

Zadanie 1. Zegarek ma wyświetlacz cyfrowy, na którym pojawiają się po dwie cyfry dla oznaczania godzin i minut. Ponadto został tak zaprogramowany, że emituje dźwięk "bip" w momencie, gdy suma cyfr na wyświetlaczu wynosi 9. Ile bipów wyemituje zegarek między 4:00 i 12:00?

Zadanie 2. Zegar cyfrowy pokazuje godziny (w systemie od 00 do 23), minuty i sekundy. Ile razy w ciągu doby wszystkie cyfry zmieniają się na tym zegarze na raz?

Zadanie 3. Na wyświetlaczu mojego zegarka cyfrowego jest godzina 02:31. Ile czasu minie zanim cyfry 0,1, 2, 3 znowu pojawią się razem na wyświetlaczu?

Zadanie 4. Na szklanym blacie biurka Beaty stoi 24-godzinny zegarek cyfrowy. O 13:08 dziewczynka zauważyła, ze jego odbicie w blacie biurka też pokazuje tę samą godzinę. Ile razy zdarza się to w ciągu doby?

Zadanie 5. Zegarek elektroniczny pokazujący godziny i minuty (godziny pokazuje do 23) leży na stole pomiędzy Jasiem i Małgosią, którzy siedzą naprzeciw siebie. Każde z nich spojrzało na zegarek i odczytało pewną godzinę. Ile czasu w ciągu doby może zajść taka sytuacja?

Zadanie 6. Na dworcu zegar cyfrowy wyświetla czas w formacie czterech cyfr (dwie dla godzin od 00 do 23 oraz dwie dla minut od 00 do 59), z których każda składa się z 7 segmentów świetlnych. Podczas 5 minut postoju pociągu podróżny liczył w każdej minucie segmenty, które zmieniały swój stan (zapalały się lub gasły). Odnotował kolejno: 4 zmiany, 1 zmianę, 11 zmian i 4 zmiany. Która godzina pojawiła się po piątej zmianie?

Zadanie 7. Zegarek elektroniczny wyświetla cyfry zapalając w danym polu do 7 kresek. Jeśli w danym polu wyświetlane są kolejno wszystkie cyfry od 0 do 9, która z kresek jest używana najmniejszą liczbę razy?

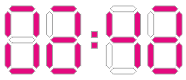Zadanie 8. Na zegarku każda cyfra jest wyświetlana jako kombinacja pewnych 7 segmentów. Może być na nim wyświetlana data lub godzina, każda w postaci dwóch liczb dwucyfrowych oddzielonych dwukropkiem. Zegarek został tak zaprogramowany, że ma możliwość jednoczesnego wyświetlania daty i godziny poprzez nałożenie odpowiednich cyfr. Na rysunku wyświetlony jest jednoczesny obraz daty 1 XII i godziny 12:47. Pewnego dnia o pewnej porze wśród ośmiu cyfr wskazujących datę i godzinę było 7 różnych cyfr bez dwójki i siódemki, zaś w trybie jednoczesnego wyświetlenia daty i godziny na ekranie pojawiły się cztery ósemki. Kiedy to się zdarzyło?

Zadanie 9. Zegarek wyświetla godziny od 0:00 do 23:59 (cyfra dziesiątek godzin wyświetla się tylko wtedy, gdy jest różna od zera). Każda cyfra jest wyświetlana jako kombinacja pewnych 7 segmentów. Na rysunku widać, jak wyświetlana jest cyfra 5, gdy nie działają segmenty oznaczone pojedynczymi kreskami. Wtedy nie można odczytać tej cyfry jednoznacznie (tak samo wyglądają 3, 7 i 9). Jaka maksymalna liczba segmentów może nie działać, żeby w każdej chwili można było odczytać, która jest godzina?

Zadanie 1. Ile razy w ciągu doby bije zegar, który wybija pełne godziny i połówki godzin?

Zadanie 2. Zegar wybija godzinę 6 w ciągu 6 sekund. Jak długo będzie wybijał godzinę 12?

Zadanie 3. W pewnym mieście godziny wybijają dwa zegary, z których pierwszy bije co dwie sekundy, a drugi co trzy, przy czym drugi zegar rozpoczyna zawsze wybijać godziny o 2 sekundy wcześniej niż pierwszy. Którą godzinę wskazywały zegary, jeżeli usłyszano 12 uderzeń?

Zadanie 1. Wczoraj Marek nastawił na właściwą godzinę stary zegar i stary budzik swojego dziadka. Dziś rano stwierdził, że zegar pokazuje godzinę 7:00, a budzik 6:00. Marek pamięta, że według słów dziadka, zegar spieszy 1 minutę na godzinę, a budzik późni 3 minuty na godzinę. O której Marek nakręcił zegar i budzik?

Zadanie 2. Zegarek babci spieszy, a dziadka późni 30 minut na godzinę. O północy oboje nastawili zegarki. O której godzinie oba zegarki pokażą znowu ten sam czas?

Zadanie 3. Zegarek Marka śpieszy 3 minuty na godzinę, a zegarek jego nauczyciela późni 5 minut na godzinę. Tego ranka oba zegarki ustawiono w tym samym momencie według dokładnego zegara na wieży ratusza. Pod koniec ostatniego obiegu tego dnia jeden zegarek wskazywał godzinę 15:55, a drugi 17:07. Która godzina była na ratuszu w momencie, gdy zegarki zostały ustawione?

Zadanie 1. Sydney poleciał na wakacje do Melbourne w Australii. Lot trwał 21 godzin. Wyleciał z Londynu o 11:30 we wtorkowe przedpołudnie. Która godzina była w Melbourne, gdy tam przyleciał?

Zadanie 2. Dziś wybieram się na wakacje do Syldawii i wykupiłem bilet na samolot, który odlatuje z Paryża o godz. 23:30 i przylatuje do Syldawii następnego dnia o godzinie 9:45 rano. Powrót zaplanowałem samolotem tej samej linii, który odlatuje z Syldawii o godzinie 11:00 i przylatuje do Paryża tego samego dnia o godzinie 15:45. Czas lotu w jedną i drugą stronę jest taki sam. Godziny odlotów i przylotów podane są według czasu lokalnego. Ile trwa lot z Paryża do Syldawii?

Zadanie 3. Okrążając kulę ziemską w kierunku wschodnim (tak jak zrobił to Phileas Fogg z powieści Juliusza Verne'a), po przekroczeniu linii zmiany daty podróżujący "znajduje się" w czasie o 24 godziny wcześniejszym, zatem człowiek okrążający Ziemię w czasie krótszym niż 24 h (co jest przecież technicznie możliwe) znajdzie się po takiej podróży w miejscu startu o czasie wcześniejszym niż ten, w którym wyruszył. Jak to możliwe?

Zadanie 1. Mamy do dyspozycji sznurek i źródło ognia. Sznurek spala się w ciągu godziny, ale wykonany jest z niejednorodnego materiału i jedne jego fragmenty palą się szybciej, a inne wolniej. Jak odmierzyć 30 minut, nie używając niczego więcej?

Zadanie 2. Mamy do dyspozycji zapalniczkę oraz dwa sznurki, z których każdy spala się w godzinę. Jak za ich pomocą odmierzyć 15 minut?

Zadanie 3. Profesor Sędziwy gotuje jajko przez 4 min, ale nie używa przy tym zwykłego zegarka, tylko dwóch klepsydr. Jedna z nich odmierza 8, a druga 3 minuty. Skąd profesor wie, kiedy jajko jest gotowe?

Zadanie 4. Jak można przygotować kalafior do sałatki, jeśli ma on być gotowany 15 min, a czas możemy mierzyć jedynie za pomocą dwóch klepsydr - 7- i 11-minutowej?