Szkoła Podstawowa Tikkun Olam
ul. Sieradzka 5, 50-568 Wrocław
tel. 71 364 60 70
www.tikkunolam.pl
e-mail: szkola@tikkunolam.pl
zgłoszenia - do 11 I 2016
eliminacje - 14 I 2016 o godz.10:00 w siedzibie Tikkun Olam
finał - 11 III 2016 godz. 10 w siedzibie Tikkun Olam
To nowa propozycja adresowana do uczniów klas III i IV szkół podstawowych. Celem zawodów jest rozwijanie zainteresowań matematycznych i umiejętności logicznego myślenia wśród najmłodszych. Zasady wzorowane są na konkursie, który pod tą samą nawą organizowany jest od kilkunastu lat w województwie śląskim przez Pracownię Matematyki i informatyki działającą w Pałacu Młodzieży w Katowicach. Na Dolnym Śląsku konkurs jest bezpłatny. Organizują go nauczyciele matematyki z zespołu szkół żydowskich Tikkun Olam. Zadania konkursowe mają w większości formę zagadek i łamigłówek logicznych. Wśród nich są problemy rozwijające wyobraźnię geometryczną np. rozmaite tangramy lub zadania o podziałach wielokątów na przystające części. Pytania mają formę testową lub otwartą. Uczniowie otrzymują karty odpowiedzi, co ułatwia im zrozumienie treści i wykonanie polecenia.
Przygotowując się do konkursu, można skorzystać z bogatej bazy zadań archiwalnych ze śląskiej edycji konkursu, bo pewne typy zadań powtarzają się z roku na rok.
Konkurs odbywa się w województwie śląskim od roku 2000 i cieszy się dużą popularnością wśród uczniów. W roku 2016 po raz pierwszy został zorganizowany na Dolnym Śląsku.
- Zgłoszenia szkół do udziału w konkursie należy przesyłać na adres mailowy szkola@tikkunolam.pl. Zgłoszone szkoły otrzymują potwierdzenie przyjęcia zgłoszenia.
- W zgłoszeniu należy podać: imię i nazwisko oraz adres mailowy i telefon kontaktowy nauczyciela, dane uczestników konkursu (imię, nazwisko, klasa), nazwę i adres szkoły z telefonem oraz e-mail do sekretariatu.
- Każda szkoła może zgłosić do eliminacji najwyżej 5 uczestników.
- Konkurs odbywa się w dwóch kategoriach wiekowych - osobno dla klas III i IV SP.
- Konkurs jest dwuetapowy. Składa sie z eliminacji i finału.
- Każdy etap trwa 45 minut.
- W eliminacjach uczniowie rozwiązują zestaw 6 zadań testowych jednokrotnego wyboru (po 4 odpowiedzi, z których jedna jest prawdziwa) i 2-3 zadania otwarte o charakterze zagadek logicznych.
- W finale uczestnicy otrzymują do rozwiązania 6 zadań otwartych o różnej trudności.
- Lista uczniów zakwalifikowanych się do finału oraz wszystkie inne informacje związane z II etapem konkursu są umieszczane na facebooku oraz wysłane pocztą elektroniczną do sekretariatów szkół uczestniczących w konkursie.
ELIMINACJE
1. Przestawiamy cyfry w numerze roku 2014 tak, aby powstały inne liczby czterocyfrowe. Na przykład 2041. Ile rożnych liczb (innych niż 2014) może powstać w ten sposób?
a) mniej niż 17 b) 17 c) 18 d) więcej niż 18
2. Która jest godzina, jeśli 15 minut temu mama zapytana o to przez Asię odpowiedziała, że za 10 minut będzie kwadrans przed 13?
a) 12:40 b) 12:45 c) 12:50 d) 12:55
3. Podziel prostokąt z rysunku wzdłuż kratek na cztery identyczne części, czyli takie, że gdybyś wyciął je wzdłuż linii podziału, to dałoby się nałożyć jedną na drugą. Jeśli potrafisz dokonać więcej takich podziałów, narysuj je wszystkie.
FINAŁ
1. Zosia, Marysia, Julia i Ada mają w domu po jednym zwierzątku - każda inne. Są to: kot, papuga, kanarek i wąż. Jakie zwierzątko ma każda z dziewcząt, jeśli wiadomo, że:
– Marysia nie lubi ptaków.
– Julia nie ma kanarka.
– Zosia ma zwierzątko o największej liczbie nóg.
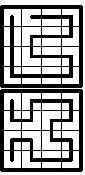2. Wędrówkę po kwadracie zaczynasz w środku lewej górnej kratki. Musisz przejść przez każdą kratkę, ale przez żadną nie możesz przejść dwa razy. Z kratki do kratki możesz przejść tylko przez bok, nigdy przez wierzchołek. Na rysunku obok narysowane są dwa różne możliwe przejścia po kwadracie zbudowanym z 16 kratek. Narysuj różne możliwości takiej wędrówki po kwadracie zbudowanym z 9 kratek.
3. Wykorzystując trzy różne liczby oraz znaki działań i nawiasy, można uzyskiwać różne wyniki. Z liczb 2, 3 i 4 można na przykład otrzymać:
14 = 2·(3+4) 10 = 2·3+4 5 = 3+4:2 6 = (4−2)·3.
Masz do dyspozycji cztery znaki: +, –, ·, : oraz trzy liczby: 1, 2, 4. Możesz również używać nawiasów. Które z liczb: od 1 do 12 potrafisz uzyskać? Podaj po jednym przykładzie.
Zadania pochodzą ze strony Pracowni Matematyki Pałacu Młodzieży i Kultury w Katowicach.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
