w Polsce
Stowarzyszenie na rzecz Edukacji Matematycznej
we Wrocławiu
Uniwersytet Ekonomiczny
ul. Komandorska 118/120, 53-345 Wrocław
e-mail: info-pl@math.naboj.org
strona domowa konkursu
junior
rejestracja: 2 X - 15 XI 2024
zawody: 22 XI 2024
senior
rejestracja: od 10 II 2025 do 5 III 2025
zawody: 14 III 2025
Miejsce:
junior -
senior
Centrum Kształcenia Ustawicznego
Uniwersytet Ekonomiczny we Wrocławiu
ul. Kamienna 57/59,
53-345 Wrocław
To międzynarodowy konkurs matematyczny adresowany do uczniów szkół średnich, rozgrywany w dwóch kategoriach wiekowych: Juniorzy (klasy I-II) oraz Seniorzy (klasy III i IV). Konkurs ma także edycję fizyczną oraz matematyczno-fizyczną wersję Junior dla klas 7-8 szkół podstawowych (tylko Polska, Czechy, Słowacja).
Zawody matematyczne rozgrywane były początkowo w Krakowie, Pradze, Opawie, Bratysławie, Koszycach, Pasawie, Linzu i Budapeszcie, od 2016 roku także w Warszawie i we Wrocławiu, a od 2018 w Białymstoku i wielu innych miastach Europy. Organizatorem edycji wrocławskiej początkowo był ZSA PWr, a od roku 2018 jest Uniwersytet Ekonomiczny.
Konkurs ma bardzo ciekawą formułę. Uczniowie rozwiązują zadania w 5-osobowych drużynach reprezentujących poszczególne szkoły. Rywalizacja polega na osiągnięciu jak największej liczby poprawnych odpowiedzi. Zadania są sprawdzane i wydawane na bieżąco. Na żywo są też transmitowane wyniki wszystkich innych drużyn biorących udział w konkursie w pozostałych miastach.
Nie ma ograniczeń na liczbę podejść z odpowiedzią do danego zadania, ale po trzeciej nieudanej próbie jury może zażądać wglądu do pełnego rozwiązania. Na starcie wszystkie drużyny otrzymują po sześć zadań, a następne, gdy poprawnie rozwiążą którekolwiek z nich. Drużyna kończy zawody po 2 godzinach lub gdy rozwiąże wszystkie przygotowane zadania, to jest ok. 50 w kategorii Junior i 40 w kategorii Senior (jedenaste zadanie dla Juniorów jest pierwszym dla Seniorów). Poziom trudności zadań rośnie wraz z ich numeracją. Początkowe zadania są stosunkowo przystępne, ale większość problemów jest niestandardowa, a ich rozwiązanie wymaga pomysłowości i inwencji. Ciekawe zadania, presja czasu, rywalizacja na żywo z innymi zespołami, współpraca w grupie czynią z tych zawodów wielce interesującą rozgrywkę.
W każdym z miast tworzony jest lokalny ranking drużyn, ale uczniowie również mogą porównać swoje wyniki w rankingu krajowym i międzynarodowym. Najlepsze zespoły otrzymują dyplomy i nagrody.
Po każdej edycji konkursu wydawany jest we wszystkich językach zbiór zadań wraz z rozwiązaniami (wersję polską wydają Wydawnictwa Szkolne Omega).
Náboj powstał w 1998 roku na Słowacji, w 2004 roku przyłączyły się Czechy, w 2014 roku Bawaria i jednorazowo Finlandia, a w 2015 roku Austria, Węgry i Polska. Liczba uczestników konkursu stale rośnie. W 2015 roku startowało w nim 458 drużyn z 6 krajów. Od 2016 roku zawody odbywają się we Wrocławiu. Dwie educje organizował Zespół Szkół Akademickich PWr. Od 2018 zawody organizuje UE. W IV edycji w 2018 roku startowało w 15 miastach europejskich (w tym 5 polskich) 988 drużyn.
Od 2012 roku organizowana jest edycja "Junior" dla szkół podstawowych, w Polsce od 2017 (tylko w Krakowie), od 2018 we Wrocławiu.
Polskie sukcesy:
- 2015
I m. kategoria Junior
GIM 24 Gdynia: Paweł Sawicki, Kacper Kluk, Wojciech Jankowski, Kacper Walentynowicz, Piotr Kowalewski
II m. kategoria Senior
XIV LO Warszawa: Mikołaj Leonarski, Tymoteusz Miara, Konrad Paluszek, Jacek Rutkowski, Michał Zawalski - 2016
I m. kategoria Junior
III LO Gdynia: Wojciech Jankowski, Kacper Kluk, Piotr Kowalewski, Paweł Sawicki, Kacper Walentynowicz
II m. kategoria Senior
XIV LO Warszawa: Leszek Sołdan, Adam Klukowski, Jakub Perlin, Tomasz Kościuszko, Marcin Korona - 2017
II m. kategoria Junior
II LO Końskie: Mateusz Basiak, Maciej Dziuba, Mateusz Górski, Mikołaj Grzebieluch, Tomasz Kosmulski
I m. kategoria Senior
III LO Gdynia: Damian Burczyk, Paweł Burzyński, Kacper Kluk, Paweł Sawicki, Antoni Żewierżejew
- 2018
III m. kategoria Junior
III LO Tarnów: Dominik Chmura, Katarzyna Kaczak, Filip Konieczny, Rafał Pyzik, Marek Zarzycki
I m. kategoria Senior
III LO Gdynia: Damian Burczyk, Kacper Kluk, Paweł Sawicki, Kacper Walentynowicz, Antoni Żewierżejew
Naboj Junior
I m. Społeczna SP 1 STO Łódź - 2019
II m. kategoria Junior
III LO Gdynia: Mateusz Scharmach, Justyna Palikowska, Michał Wiliński, Kajetan Lewandowski, Franciszek Sulima
I m. kategoria Senior
V LO Kraków: Radosław Żak, Tomasz Ślusarczyk, Piotr Kubaty, Piotr Ryłko, Michał Woźny
Naboj Junior
V m. SP 1 Białystok: Bartosz Bielawiec, Michał Buczyński, Paweł Buczyński, Konrad Zajczyk - 2020
I m. kat. Senior
V LO Kraków: Tomasz Ślusarczyk, Radosław Żak, Kacper Paciorek, Mateusz Nowak, Daniel Goc
I m. kat. Junior
III LO Ww:
Antoni Buraczewski, Jan Pezda, Cyprian Ziółkowski, Wojciech Sobiński, Łukasz Besuch
Naboj Junior - konkurs odwołany ze względu na epidemię koronawirusa. - 2021
I m. kat. Senior
V LO Kraków: Radosław Żak, Witold Sikora, Kacper Paciorek, Kosma Kasprzak, Stanisław Sieniawski
I m. kat. Junior
III LO Ww: Antoni Buraczewski, Jan Pezda, Wojciech Sobiński, Kuba Walęga, Cyprian Ziółkowski
Naboj Junior
VIII m. SP 53 Białystok: Grzegorz Wojciuk, Kacper Januszkiewicz, Stanisław Kozłowski, Adam Sienkiewicz - 2022
I m. kat. Senior
V LO Kraków: Kosma Kasprzak, Kacper Paciorek, Witold Sikora, Maja Kokot, Krzysztof Salata
I m. kat. Junior
XIV LO Warszawa: Zofia Adamowska, Bartosz Stopczyński, Kajetan Ramsza, Jan Kaszycki, Jan Gwiazda
Naboj Junior
V m. SP 221 Warszawa: Jakub Zagrodzki, Tomasz Ostrowski, Antoni Chwiejczak, Jerzy Fronczyk - 2023
I m. kat. Senior
III LO Wrocław: Antoni Buraczewski, Jan Pezda, Wojciech Sowiński, Kuba Walęga, Cyprian Ziółkowski
I m. kat. Junior
V LO Kraków: Magdalena Pudełko, Miłosz Płatek, Kordian Pisarek, Antoni Mazur, Szymon Wróblewski
Naboj Junior
II m. na świecie SP 221 Warszawa: Jakub Zagrodzki, Tomasz Ostrowski, Antoni Chwiejczak, Jerzy Fronczyk - 2024
I m. kat. Senior
XIV LO Warszawa: Jan Gwiazda, Kajetan Ramsza, Krzysztof Pietrusiak, Jeremi Hyska, Robert Soboński
I m. kat. Junior
V LO Kraków: Antoni Mazur, Tymon Sidor, Juliusz Marszałek, Błażej Dratwa, Jan Kosiorowski
Naboj Junior
I m. na świecie SP 221 Warszawa: Dominik Findeisen, Krzysztof Kowalik, Artur Smoleński, Szymon Zima - 2025
Wrocławskie sukcesy:
- 2015
VII m. w Polsce na 28, XIII m. na świecie na 219 w kategorii Senior
XIV LO Ww: Wojciech Fica, Kamil Górecki, Maciej Kucharski, Piotr Pusz, Martyna Siejba - 2016
VII m. w Polsce na 106, X m. na świecie na 414 w kategorii Junior
III LO Ww: Dawid Ignasiak, Karol Kuczmarz, Mateusz Marecki, Mikołaj Marsy, Mateusz Rzepecki
XIV m. w Polsce na 77, XVII m. na świecie na 336 w kategorii Senior
III LO Ww: Grzegorz Ciesielski, Antoni Kamiński, Maciej Korpalski, Michał Szachniewicz, Barbara Zięba - 2017
X m. w Polsce na 126, XVIII m. na świecie na 450 w kategorii Junior
GA PWr Ww: Zofia Stypułkowska, Łukasz Orski, Mateusz Padarz, Adam Pędziwiatr, Szymon Szecówka
VII m. w Polsce na 99, XIV m. na świecie na 405 w kategorii Senior
III LO Ww: Maciej Korpalski, Dawid Ignasiak, Mateusz Rzepecki, Katarzyna Miernikiewicz, Michał Kucharczyk - 2018
III m. w Polsce na 147, V m. na świecie na 490 w kategorii Junior
III LO Ww: Łukasz Caliński, Aleksandra Ciura, Mateusz Kapusta, Łukasz Krzempek, Krzysztof Olejniczak
XVI m. w Polsce na 128, XXV m. na świecie na 486 w kategorii Senior
III LO Ww: Dawid Ignasiak, Jakub Kamiński, Adam Morawski, Mateusz Rzepecki, Andrzej Turko
Nabój Junior
V m. w Polsce na 197, XVIII m. na świecie na 987
SP 3 Ww: Tomasz Gąciarz, Maja Omelaniuk, Jan Pezda, Andrzej Pijanowski - 2019
III m. w Polsce na 115, IV m. na świecie na 499 w kategorii Senior
III LO Ww: Łukasz Krzempek, Jakub Kamiński, Mateusz Kandybo, Krzysztof Olejniczak, Iwo Pilecki-Silva
IV m. w Polsce na 121, V m. na świecie na 496 w kategorii Junior
LA PWr Ww: Łukasz Orski, Kacper Misiaszek, Łukasz Świszcz, Łukasz Pawlik, Karol Janic
Naboj Junior
IV m. w Polsce na 155, XVIII m. na świecie na 905
SP 3 Ww: Bartosz Bielawiec, Michał Buczyński, Paweł Buczyński, Konrad Zajczyk - 2020
III m. w Polsce na 134, VI m. na świecie na 363 w kategorii Senior
III LO Ww: Łukasz Caliński, Mateusz Kapusta, Łukasz Krzempek, Krzysztof Olejniczak, Iwo Pilecki-Silva
I m. w Polsce na 211, I m. na świecie na 569 w kategorii Junior
III LO Ww: Antoni Buraczewski, Jan Pezda, Cyprian Ziółkowski, Wojciech Sobiński, Łukasz Besuch
Naboj Junior - konkurs odwołany ze względu na epidemię koronawirusa. - 2021
I m. na świecie na 591 drużyn w kategorii Junior
III LO Wrocław: Antoni Buraczewski, Jan Pezda, Wojciech Sobiński, Kuba Walęga, Cyprian Ziółkowski
IV m. na świecie na 547 drużyn w kategorii Senior
ALO PWr: Łukasz Orski, Kacper Misiaszek, Łukasz Jałocha, Bartłomiej Bychawski, Jakub Rudzik
Naboj Junior
VI m. w Polsce na 336, 38 m. na swiecie na 1085
SP 10 Wrocław: Łukasz Ganczarek, Maximilian Ogorzelski, Filip Szlązak, Maksymilian Troska - 2022
IV m. w Polsce na 201 drużyn (i IV na świecie na 622) w kategorii Senior
III LO Wrocław: Antoni Buraczewski, Jan Pezda, Wojciech Sobiński, Kuba Walęga, Cyprian Ziółkowski
IV m. w Polsce na 179 drużyn (i V na świecie na 717) w kategorii Junior
XIV LO Wrocław: Rafał Mańczyk, Marek Muzyka, Jakub Nowak, Wojciech Rybak, Miłosz Dudała
Naboj Junior
II m. w Polsce na 144 drużyny (i 20 na świecie na 1414)
SP 3 Wrocław: Piotr Lecyk, Szymon Czapliński, Monika Izworska, Szymon Tkocz - 2023
I m. na świecie w kategorii Senior (na 468 drużyn)
III LO Wrocław: Antoni Buraczewski, Jan Pezda, Wojciech Sobiński, Kuba Walęga, Cyprian Ziółkowski
VI m. na świecie w kategorii Junior (na 479 drużyn)
ALO PWr: Mateusz Wawrzyniak, Urszula Wojtasik, Jakub Gaj, Błażej Chamuczyński, Franciszek Jarzembowski
Naboj Junior
V m. w Polsce SP 3 Wrocław: Michał Maciołka, Tymon Mikita, Mariia Kulyk, Szymon Śpiewak
VI m. w Polsce SP 3 Wrocław: Jakub Matuszewski, Małgorzata Mikołajczyk, Nadia Ochędzan, Ida Ochnik - 2024
VII m. na świecie w kategorii Senior (na 602 drużyny)
XIV LO Ww: Marek Muzyka, Jakub Nowak, Paulina Żeleźnik, Rafał Mańczyk, Wojciech Rybak
X m. na świecie w kategorii Junior (na 644 drużyny)
ALO PWr: Rafał Żebruń, Marcin Laskowski, Mateusz Tokarski, Maria Czerwińska, Zofia Tłuczek
Naboj Junior
VIII m. w Polsce (na 314 drużyn)
SP 82 Wrocław: Franciszek Mroziński, Tomasz Szmidt, Jaraslau Sialiuk i Aleksandr Petrov - 2025
- Konkurs matematyczny Naboj adresowany jest do uczniów szkół średnich.
- Zawody są drużynowe i przeprowadzane w dwóch kategoriach: Juniorzy - kl. I i II oraz Seniorzy – kl. III i IV.
- Szkoła może zgłosić w każdej kategorii jedną drużynę poprzez stronę internetową organizatora i wybrać miejsce zawodów w swoim kraju. Drużyny mogą być 4- lub 5-osobowe.
- Zgłoszenie dodatkowej drużyny w każdej kategorii przysługuje szkołom, które zajęły pierwsze trzy miejsca w rankingu krajowym w poprzednim roku.
- Każdy okręgowy organizator podaje limit liczby przyjmowanych drużyn.
- Zawody trwają 2 godziny. Trudność zadań wzrasta wraz z ich numeracją.
- Na starcie każda drużyna otrzymuje sześć zadań. Odpowiedzi numeryczne są sprawdzane na bieżąco. Uczestnicy otrzymują kolejne zadanie, gdy rozwiążą poprawnie przynajmniej jedno zadanie poprzednie. Nie ma ograniczeń na liczbę oddawanych odpowiedzi do danego zadania, ale po trzeciej nieudanej próbie juror może zażądać od zawodnika pełnego rozwiązania.
- Tworzone są rankingi międzynarodowe, krajowe i lokalne. Wygrywa drużyna, która rozwiąże najwięcej zadań. Jeśli wiele drużyn rozwiązało tyle samo zadań, zwycięzcą jest ta, która rozwiązała zadanie o najwyższym numerze. W przypadku gdy dalej jest remis, rozstrzyga drugi najwyższy numer rozwiązanego zadania itd. W przypadku gdy wiele drużyn rozwiązało dokładnie te same zadania, zwycięża drużyna, która w najkrótszym czasie złożyła ostatnie zadanie.
- Konkurs matematyczno-fizyczny Naboj-Junior adresowany jest do uczniów klas 7 i 8 szkół podstawowych. Jego zasady są analogiczne jak w Naboju.
Senior
1. Pijąc szklankę czarnej herbaty, zyskuje się kofeinę na 1 godzinę. Pijąc szklankę kawy, zyskuje się kofeinę na 4 godziny. W jakim stosunku należy wymieszać czarną herbatę i kawę, by uzyskać pełną szklankę napoju zawierającą kofeinę na 2 godziny?
2. Ulubiona liczba Natalii ma wszystkie poniższe własności. Jaka to liczba?
- ma 8 różnych cyfr
- cyfry czytane od lewej do prawej występują w kolejności malejącej
- jest podzielna przez 180.
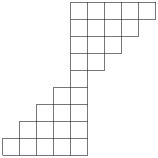3. Żaba porusza się po diagramie składającym się 29 kwadratów jednostkowych. W każdym kroku skacze albo do kwadratu przylegającego powyżej (jeśli taki istnieje), albo do kwadratu znajdującego się bezpośrednio powyżej i po prawej od jej obecnej pozycji (jeśli taki istnieje). Żaba zaczyna w jednym z pięciu kwadratów w dolnym rzędzie i skacze dopóki nie dojdzie do górnego rzędu. Ile różnych ścieżek od dolnego do górnego rzędu może obrać?
4. Składamy prostokątną kartkę papieru w taki sposób, żeby dwa przeciwległe rogi (po przekątnej) pokryły się, tworząc w ten sposób zgięcie, czyli odcinek widoczny na papierze. Okazuje się, że długość tego zgięcia jest taka sama jak długość dłuższego boku prostokąta. Jaki jest stosunek długości dłuższego boku do krótszego boku prostokąta?
5. Wyobraźmy sobie klatkę dla królików utworzoną z 7×7 komórek. Na ile sposobów możemy umieścić tam 8 nierozróżnialnych zrzędliwych królików tak, aby każde dwa króliki były oddalone od siebie o co najmniej 3 komórki w pionie lub co najmniej 3 komórki w poziomie?
Junior
1. Jola kupiła niedawno aparat fotograficzny. Zapłaciła za niego 212,30 złotych banknotem 500 zł. Jaka jest najmniejsza liczba banknotów i monet, jaką może jej wydać kasjerka?
2. Wieża została umieszczona na jednym z pól pustej szachownicy o wymiarach 8x8. Ile jest pól, na które możemy przenieść wieżę, wykonując jeden ruch? Wieża może poruszać się tylko w pionie lub w poziomie.
3. Pan Adam wraca z wakacji. Jedzie samochodem do miasta, które jest oddalone o 250 km. Przez pierwszą godzinę porusza się ze średnią prędkością 50 km/h. Z jaką prędkością powinien przejechać resztę drogi, aby średnia prędkość całej podróży podwoiła się w stosunku do średniej prędkości z pierwszej godziny? Wynik zaokrąglij w dół do pełnych km/h.
4. Piotr sprawdzał wagę ciężarków atletycznych. Najpierw zważył na raz trzy z nich, o masach odpowiednio 0,03 t, 200 000 g i 15 kg. Potem wziął inne trzy ciężarki o masach 0,01 t, 35 000 g i 200 kg. Jaka jest różnica mas pomiędzy dwiema grupami ciężarków, które ważył Piotr?
5. Kran w łazience Radka przecieka. Chłopiec zmierzył, że co dwie sekundy spada jedna kropla. Po tym, jak tato Radka naprawił kran, krople wody spadały już tylko co dziewięć sekund. Oblicz stosunek częstotliwości spadania kropli przed i po naprawieniu kranu.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
