Od stycznia 2014 zadania Ligi Zadaniowej dla Gimnazjów należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Stado liczy dziesięć kóz w różnym wieku. Pierwsza koza zjada balot siana w jeden dzień, druga - w dwa dni, trzecia - w trzy dni itd. Każda następna koza zjada balot siana o dzień dłużej, tak że dziesiąta koza zjada go w dziesięć dni. Ile czasu będą jadły balot siana dwie pierwsze kozy razem? Ile czasu zajmie to wszystkim pozostałym kozom razem?
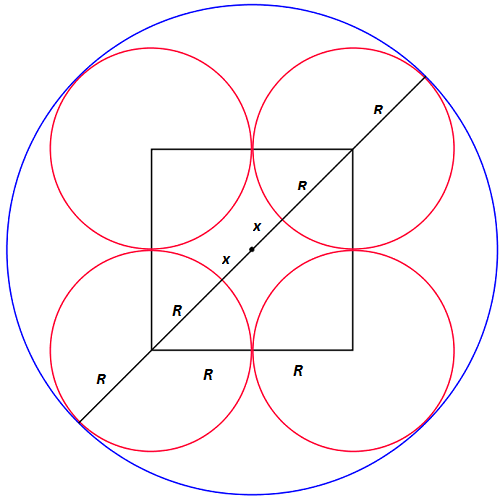
Zad. 2. Jaką maksymalną zewnętrzną średnicę może mieć słoik, aby cztery takie słoiki zmieściły się w garnku o promieniu wewnętrznym r?
Zad. 3. Rozwiąż poniższy układ nierówności i przedstaw jego rozwiązanie graficznie.
[tex]\left\{ \begin{array}{ll}
\frac{33-x}{0,5}+10>50 & \\
\frac{x}{2}-\frac{1-x}{3}<5+2x &\\
3x-5<2(x-2) & \end{array} \right.[/tex]
W tym miesiącu punkty zdobyli:
- 3 pkt. - Joanna Lisiowska KZE Warszawa, Przemysław Rybarczyk GM Stargard Szczeciński i Michał Stempniak GMSS Ostrów Wielkopolski,
- 2,5 pkt. - Bartosz Czyżewski GM 1 Jelenia Góra i Wojciech Wiśniewski GM 3 Giżycko,
- 2 pkt. - Klaudia Marcinkiewicz GM 24 Katowice.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Zwycięzcą tegorocznej Ligi Zadaniowej dla Gimnazjów z wynikiem 26,5 pkt. (na 27 możliwych) został Bartosz Czyżewski z GM 1 w Jeleniej Górze. Kolejne miejsca zajęli:
- Michał Stempniak (25,5 pkt)
- Joanna Lisiowska (24,5 pkt)
- Klaudia Marcinkiewicz (21,5 pkt)
- Wojciech Wiśniewski (20,5 pkt)
- ex aequo Maciej Pająk i Mateusz Rzepecki (15,5 pkt)
- Przemysław Rybarczyk (13,5)
Gratulujemy!
Zad. 1. Pierwsza koza zjada siano z szybkością 1 balot/dzień, a druga z szybkością 0,5 balot/dzień. Razem zjadają siano z szybkością 1,5 balot/dzień, zatem czas potrzebny obu kozom na zjedzenie balotu siana to 1/1,5 = 2/3 dnia =16 godzin. Szybkość zjadania siana przez pozostałe kozy razem wynosi 1/3 + 1/4 +...+ 1/10 = 3601/2520 balot/dzień, czyli jeden balot siana będą jadły w czasie 2520/3601 dnia = 16 godzin 47 minut 43737/3601 sekundy.
Zad. 2. Poniższy rysunek przedstawia optymalne ustawienie 4 słoików w garnku. Wewnętrzny promień garnka wynosi wtedy r = 2·R+x, gdzie R to zewnętrzny promień słoika. Zauważmy, że przekątna kwadratu o boku 2R wynosi wtedy 2R+2x. Zatem jej połowa to R+x = R√2. Stąd x = R·(√2-1). Podstawiając ten wynik do wzoru r = 2·R+x, dostajemy r = 2·R + R·(√2-1) = R·(√2+1). Stąd wyliczamy R = r/(√2+1) = r(√2-1). Czyli maksymalna zewnętrzna średnica słoika wynosi 2r(√2-1).
Zad. 3. Po uproszczeniu każdej z nierówności otrzymujemy układ równoważny:
[tex]\left\{ \begin{array}{ll}
x<13 & \\
x>-\frac{32}{7}=-4\frac{4}{7} &\\
x<1 & \end{array} \right.[/tex]
Jego rozwiązaniem jest przedział (-44/7, 1) przedstawiony na rysunku.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
