Od stycznia 2014 zadania Ligi Zadaniowej dla Gimnazjów należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
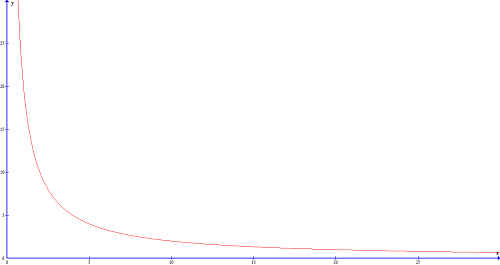
Zad. 1. Naszkicuj wykres funkcji opisującej zależność między długością jednej przekątnej w zależności od długości drugiej przekątnej deltoidu wypukłego o polu równym 10 cm2.
Zad. 2. Rozwiąż równanie (x+22014)2-41008-(x-22014)2 = 0 w liczbach rzeczywistych.
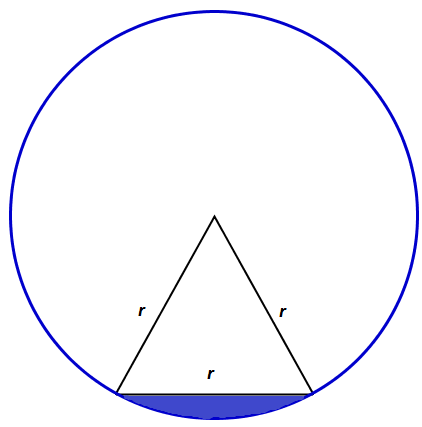
Zad. 3. W jakim stosunku cięciwa równa promieniowi koła dzieli jego pole? Podaj wartość dokładną i przybliżoną do trzech cyfr znaczących.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Bartosz Czyżewski GM 1 Jelenia Góra, Joanna Lisiowska KZE Warszawa i Michał Stempniak GMSS Ostrów Wielkopolski,
- 2,5 pkt. - Przemysław Rybarczyk GM Stargard Szczeciński, Mateusz Rzepecki GM 14 Wrocław i Wojciech Wiśniewski GM 3 Giżycko,
- 2 pkt. - Klaudia Marcinkiewicz GM 24 Katowice.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po ośmiu miesiącach Ligi z wynikiem 24 pkt. (na 24 możliwe!) prowadzi Bartosz Czyżewski z GM 1 Jelenia Góra. Gratulujemy!
Zad. 1. Oznaczając przekątne deltoidu jako x i y, otrzymujemy pole x·y/2 = 10, zatem szukana funkcja to jedna gałąź hiperboli y = 20/x.
Zad. 2. Korzystając ze wzorów skróconego mnożenia, możemy równanie uprościć do postaci 2·x·22014 + 2·x·22014 = 41008, co po przekształceniu daje x·22016 = 22016, skąd widać, że x musi być równe 1.
Zad. 3. Pole wycinka koła opartego na cięciwie o długości r jest 1/6 pola koła, czyli wynosi PW = 1/6πr2. Pole odcinka koła opartego na tej cięciwie (zaznaczony na rysunku na niebiesko) jest różnicą pola wycinka koła i pola trójkąta równobocznego o boku r, zatem wynosi ono PO = PW - PΔ = 1/6πr2 -√3/4r2 = r2/2·(π/3 - √3/2). Reszta koła to różnica całego koła i jego odcinka, a jej pole wynoai PR = πr2 - PO = r2/2·(5π/3 + √3/2). Szukany stosunek pól to [tex]\frac{P_R}{P_O}=\frac{10\pi+3\sqrt{3}}{2\pi-3\sqrt{3}}[/tex]≈ 33,7.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
