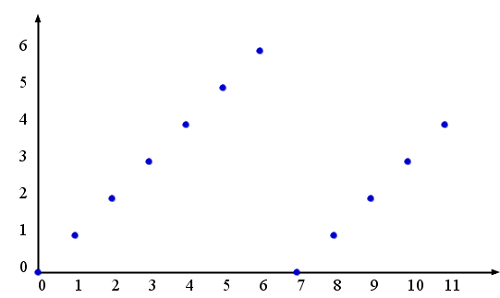
Zad. 1. Każdej liczbie naturalnej przyporządkowana jest reszta z jej dzielenia przez 7. Jaki jest zbiór wartości tej funkcji? Naszkicuj wykres tej funkcji dla argumentów mniejszych od 12.
Zad. 2. Rozwiąż równanie [tex]\sqrt{x^x}=x^{\sqrt{x}}[/tex].
Zad. 3. Punkt A leży we wnętrzu kąta ostrego. Znajdź punkty B i C leżące na ramionach tego kąta i takie, aby obwód trójkąta ABC był najmniejszy.
W tym miesiącu punkty zdobyli:
- 2,5 pkt. - Kacper Gembara ZSS Wołów, Konrad Litwiński G 86 Warszawa, Zofia Ogonek G 58 Warszawa i Mateusz Rzepecki G 14 Wrocław,
- 2 pkt. - Oliwia Kropidłowska G 1 Wrocław, Joanna Lisiowska KZE Warszawa, Przemysław Rybarczyk G Integracyjne Stargard Szczeciński, Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski i Krzysztof Żmuda G Wieczfnia Kościelna,
- 1 pkt. - Łukasz Pawlak G Dwujęzycze Oborniki Śląskie.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Po dziewięciu miesiącach Ligi Zadaniowej z wynikiem w czołówce znaleźli się (w nawiasach podajemy liczby zdobytych punktów na 27 możliwych):
I m. (26,5) - Konrad Litwiński
II m. (25,5) - Mateusz Rzepecki i Michał Stempniak
III m. (25) - Kacper Gembara
IV m. (24,5) - Zofia Ogonek
V m. (23,5) - Oliwia Kropidłowska i Przemysław Rybarczyk
VI m. (21) - Joanna Lisiowska
VII m. (19,5) - Krzysztof Żmuda
VIII m. (17) - Łukasz Pawlak
IX m. (15,5) - Aleksandra Domagała G 23 Wrocław
X m. (14) - Magdalena Owczarek, G Legionowo
XI m. (13,5) - Iwo Pilecki-Silva, G 26 Wrocław
XII m. (9,5) - Helena John, G Wielowieś
Gratulujemy!
Zad. 1. Zbiór wartości funkcji to {0, 1, 2, 3, 4, 5, 6}. Jej wykres dla argumentów całkowitych niejszych od 12 przedstawiono poniżej. Dla argumentów naturalnych funkcja jest okresowa.
Zad. 2. Zauważmy, że dziedziną równania są liczby dodatnie (ujemne nie mogą być wstawione pod pierwiastek kwadratowy, a przyjęcie x=0 prowadzi do wielkości nieoznaczonej 00). Dla x>0 równanie przyjmuje postać [tex]x^{\frac{x}{2}}=x^{\sqrt{x}}[/tex]. Łatwo zaobserwować, że liczba 1 spełnia równanie. Dla pozostałych podstaw wyrażenie wykładnicze jest różnowartościowe, wystarczy więc porównać wykładniki obu stron równania. Otrzymujemy [tex]\frac{x}{2}=\sqrt{x}[/tex], co jest dla liczb dodatnich równoważne warunkowi x2–4x=0, czyli x(x–4)=0. Pierwiastkami tego równania są liczby 0 i 4, ale pierwszy z nich należy odrzucić, bo nie należy do dziedziny wyjściowego równania. Zatem rozwiązaniem równania jest zbiór {1, 4}.
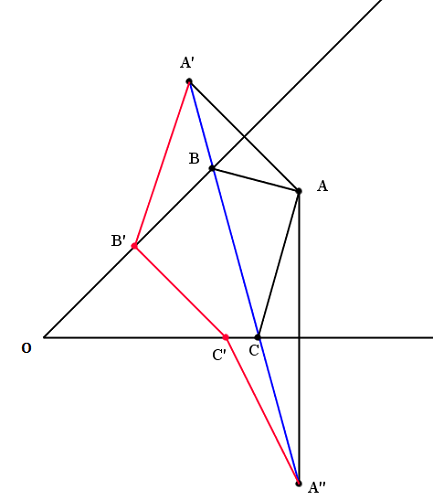
Zad. 3. Znajdujemy punkty A' i A" symetryczne do A względem ramion kąta. Prowadzimy prostą A'A". Punkty B i C to przecięcia prostej A'A" z ramionami kąta. (Uwaga! Prosta A'A" zawsze przetnie ramiona kąta ostrego, ponieważ miara kąta A'OA" jest dwa razy większa od miary kąta BOC, która nie przekracza 90°, więc kąt A'OA" jest mniejszy od półpełnego - za brak tej argumentacji odejmowaliśmy 0,5 pkt). Ponieważ ramiona kąta są symetralnymi odcinków AA' i AA", trójkąty AA'B oraz AA"C są równoramienne, przy czym |AB|=|A'B| oraz |AC|=|A"C|. Stąd obwód trójkąta ABC jest równy długości odcinka A'A''. Gdyby punkty B i C zostały wybrane w innych miejscach na ramionach kąta, np. jako B' i C', to obwód trójkąta ABC byłby równy długości czerwonej łamanej A'B'C'A" (bo trójkąty AA'B' oraz AA"C' też są równoramienne). Ale odcinek jest najkrótszą z dróg łączących dwa punkty, więc łamana A'B'C'A" jest dłuższa.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
