Zad. 1. Udowodnij, że jeśli liczba naturalna jest iloczynem trzech kolejnych liczb naturalnych, to jest także sumą trzech kolejnych liczb naturalnych.
Zad. 2. W Abecadłowie mieszka 120 uczniów, a w Becadłowie - 100 uczniów. W połowie drogi pomiędzy tymi miejscowościami leży Cadłów, w którym mieszka 110 uczniów. Gdzie należy zbudować szkołę gminną, aby uczniowie z tych trzech miejscowości w drodze na lekcje pokonywali w sumie najmniej kilometrów?
Zad. 3. Jaki jest promień kuli stycznej zewnętrznie do kuli wpisanej w sześcian o krawędzi a i jednocześnie stycznej do trzech ścian tego sześcianu?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kacper Gembara G w ZSS Wołów, Oliwia Kropidłowska G 1 Wrocław, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Zofia Ogonek G 58 Warszawa, Łukasz Pawlak G Dwujęzyczne Oborniki Śląskie, Przemysław Rybarczyk G Integracyjne Stargard Szczeciński, Mateusz Rzepecki G 14 Wrocław i Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski;
- 2,5 pkt. - Krzysztof Żmuda G Wieczfnia Kościelna;
- 2 pkt. - Konrad Bartosiewicz G Topola Królewska i Wojciech Misiak G Topola Królewska;
- 1,5 pkt. - Magdalena Owczarek G Dwujęzyczne Legionowo;
- 1 pkt. - Helena John G Wielowieś.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Po ośmiu miesiącach Ligi Zadaniowej z wynikiem 24 pkt. (na 24 możliwych) prowadzi Konrad Litwiński, drugie miejsce z wynikiem 23,5 pkt. zajmuje Michał Stempniak, a trzecie z wynikiem 23 pkt. - Mateusz Rzepecki. Gratulujemy!
Zad. 1. Liczba naturalna n jest iloczynem trzech kolejnych liczb naturalnych. Wśród tych liczb jedna jest podzielna przez 3 (bo co trzecia liczba naturalna dzieli się przez 3), stąd n jest również podzielna przez 3. Dlatego n można zapisać jako sumę trzech kolejnych liczb naturalnych jako (n/3-1) + n/3 + (n/3+1).
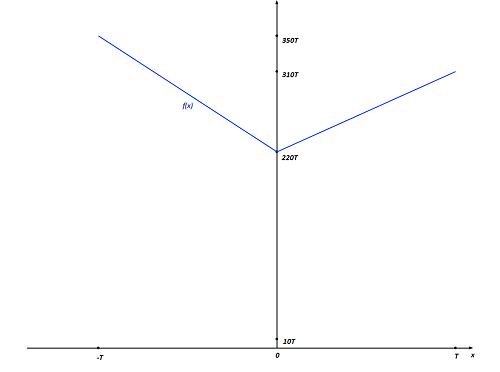
Zad. 2. Oznaczmy odległość między Abecadłowem a Cadłowem i pomiędzy Cadłowem a Becadłowem przez T [km]. Powiedzmy że postanowiliśmy zbudować szkołę w odległości x od Cadłowa, gdzie -T ≤ x ≤ T. Wtedy funkcja opisująca liczbę kilometrów łącznie pokonywanych przez dzieci to
f (x) = 120(T - x) + 110|x| + 100(T + x) = 220T - 20x + 110|x|.
Jej minimum wypada w x=0 i wynosi f (0) = 220T, co widać z poniższego wykresu.
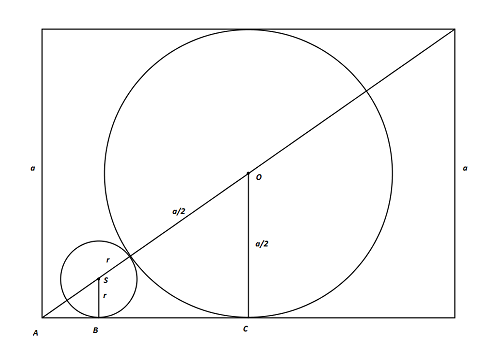
Zad. 3. Na rysunku poniżej jest przedstawiony przekrój sześcianu i obu kul wykonany wzdłuż przekątnej podstawy tego sześcianu. Z podobieństwa trójkątów ABS i ACO mamy $$\frac{r}{\frac{a}{2}}=\frac{\frac{\sqrt{3}a}{2}-\frac{a}{2}-r}{\frac{\sqrt{3}a}{2}}.$$Po przekształceniach dostaniemy [tex]r=\frac{a(2-\sqrt{3})}{2}[/tex].
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
