Zad. 1. Siostra jest o trzy lata młodsza od brata. Brat ma obecnie 2 razy tyle lat, ile miała siostra wtedy, gdy brat miał tyle, ile ma siostra teraz. Ile lat ma siostra, a ile brat?
Zad. 2. Długości boków pewnego trójkąta prostokątnego są trzema kolejnymi liczbami naturalnymi parzystymi. Oblicz pole tego trójkąta.
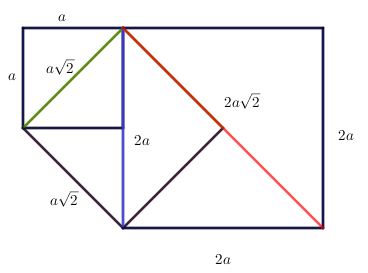
Zad. 3. Dany jest kwadrat o boku długości a. Przekątna tego kwadratu jest bokiem drugiego kwadratu. Przekątna drugiego kwadratu jest bokiem trzeciego kwadratu. Jaka jest długość przekątnej trzeciego kwadratu?
W czerwcu punkty zdobyli:
- 3 pkt. – Adam Chowanek SP Mieroszów, Emilia Cichowska SP 14 Lubin, Wojciech Domin SP Pisarzowice, Michał Dźwigaj SP 1 Przemków, Paulina Hołodniuk SP 2 Wołów, Wiktoria Jaguszczak SP Grębocice, Sandra Łuczak SP 107 Wrocław, Antoni Maracewicz SP Aslan Głogów, Paweł Michałowski PrSP 1 Białystok, Tymoteusz Noremberg SP 29 Wrocław, Lena Nowacka SP 28 Wałbrzych, Michał Plata SP 2 Syców, Tymosz Srokosz SP 52 Warszawa, Michał Węgrzyn SP 9 Wrocław, Aleksandra Wiercińska SP Raszówka, Szymon Wróbel SSP Gliwice;
• 2 pkt. – Cezary Rębiś SP Jedlnia Letnisko, Filip Timofiejczuk SP 3 Tarnowskie Góry.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Obecnie siostra ma x lat, więc brat ma (x+3). Jednocześnie z warunków zadania wynika, że brat ma 2(x–3) lata, czyli otrzymujemy równanie 2(x–3) = x+3, skąd x=9. Brat ma 12 lat, siostra ma 9 lat.
Zad. 2. Oznaczmy długości boków trójkąta a = 2n–2, b = 2n, c = 2n+2, gdzie n>1 jest liczbą naturalną. Zgodnie z twierdzeniem Pitagorasa a2+b2 = c2, otrzymujemy więc równanie (2n–2)2+(2n)2 = (2n+2)2. Po przekształceniach otrzymujemy 4n2–16n = 0, czyli n(n–4) = 0, skąd n=0 lub n=4. Warunkom zadania odpowiada tylko liczba 4. Wobec tego a=6, b=8, c=10. Pole trójkąta wynosi ½·6·8 = 24.
Zad. 3. Oznaczmy przez pi przekątną i-tego kwadratu. Wówczas p1= a√2 , p2= a√2·√2 = 2a, p3= 2a√2. Przekątna ma długość 2a√2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
