Zad. 1. W pewnej wiosce mieszkają 33 rodziny. Każda z nich ma jedno, dwoje lub troje dzieci. Liczba rodzin posiadających troje dzieci jest taka sama, jak liczba rodzin posiadających jedno dziecko. Ile dzieci jest w tej wiosce?
Zad. 2. Aby otrzymać wynik dzielenia pewnej liczby czterocyfrowej przez 65, wystarczy skreślić w niej cyfrę tysięcy. Ile wynosi ta liczba?
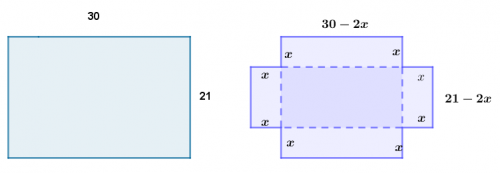
Zad. 3. Z prostokątnego arkusza kartonu o wymiarach 30 cm na 21 cm z każdego rogu wycięto kwadrat, tak, że z pozostałej części, zaginając krawędzie, złożono otwarte pudełko o pojemności 1080 cm2. Jaka jest powierzchnia każdego z wyciętych kwadratów?
W czerwcu punkty zdobyli:
- 3 – Hanna Adamska SP Parnas Wrocław, Natalia Czurejno SP Wykroty, Maja Dałek SP 44 Wrocław, Mateusz Galik SP Arka Wrocław, Igor Gawrzoł, SP Aslan Głogów, Rafał Frankowski SP 139 Warszawa, Aleksandra Koziej SP Jarczew, Wiktor Kuczaj SP 7 Nowa Ruda, Joanna Nowakowska SP 3 Głogów, Wiktoria Pietrzak SP 3 Głogów, Arkadiusz Piwowarczyk SP 14 Ostrowiec Świętokrzyski, Adrian Przygodzki SP Strzelce, Gabriela Pułecka SP 2 Brzeg Dolny, Szymon Ryś SP 16 Wrocław, Oliwia Stańczyk SP Aslan Głogów, Tytus Szczapa SP Młody Kopernik Wałbrzych, Dominika Wojdacz SP 11 Inowrocław, Anastasia Yakovleva SP 3 Mogilno;
- 2 – Aleksander Masztalski SP 3 Mikołów;
- 1 – Martyna Burnos SP 3 Głogów,
Zad. 1. Przyjmijmy oznaczenia x – liczba rodzin mających jedno dziecko, y – liczba rodzin mających dwoje dzieci, z – liczba rodzin mających troje dzieci. Z treści zadnia otrzymujemy x+y+z=33 i x=z, a stąd otrzymujemy 2x+y=33, czyli y=33-2x. Liczba dzieci w tej wiosce jest równa 1x+2y+3z=1x+2(33-2x)+3x=x+66-4x+3x=66. W tej wiosce jest 66 dzieci.
Zad. 2. Niech skreśloną cyfrą tysięcy będzie a. Liczbę x można zapisać jako 1000a+b, gdzie b jest pewną liczbą naturalną co najwyżej trzycyfrową i jednocześnie wynikiem dzielenia x przez 65. Mamy, więc 1000a+b=65b, stąd 64b=1000a, czyli b=15a:8. Ponieważ a i b są dodatnimi liczbami naturalnymi i a≤9, więc a=8 i wtedy b=125. Szukana liczba to 8125.
Zad. 3. Z warunków zadania wynika, że dno pudełka ma wymiary 30-2x i 21-2x. Ponieważ wymiary pudełka są liczbami dodatnimi, więc x>0 i 30-2x i 21-2x>0, zatem x ∈ (0; 10,5). Objętość pudełka wynosi 1080, więc (30-2x)(21-2x)x=1080.Po przekształceniu otrzymujemy równanie 4x3-102x2+630x-1080=0, skąd x(4x2-90x+360)-3(4x2-90x+360)=0, czyli (x-3)(4x2-90x+360)=0. Otrzymujemy więc dwa równania x-3=0 lub 4x2-90x+360=0. Rozwiązaniem pierwszego równania jest x1=3. Równanie kwadratowe ma dwa rozwiązania niewymierne [tex] x_2=\frac{45-3\sqrt{65}}{4} \approx5,2 [/tex], [tex] x_3=\frac{45+3\sqrt{65}}{4} \approx17,3 [/tex]. Ostatnie rozwiązanie nie spełnia warunków zadania. Zatem pole każdego z wyciętych kwadratów wnosi 9 cm2 lub około 27 cm2
