Zad. 1. Do sześciu paczek włożono czekolady w taki sposób, że każda paczka zawiera inną liczbę czekolad, ale nie większą niż sześć. Andrzej, Bartek i Czarek otrzymali po dwie takie paczki i okazało się, że Andrzej ma osiem czekolad, Bartek - dziesięć, a Czarek trzy. Po ile czekolad było w każdej paczce Bartka?
Zad. 2. Z dwóch miejscowości wyruszają ku sobie turyści, idąc ze stałymi prędkościami. Pierwszy po spotkaniu szedł do celu, z którego wyruszył drugi, jeszcze 4 godziny, a drugi szedł jeszcze 2 godziny 15 minut do celu, z którego wyruszył pierwszy. Ile czasu zajęła wędrówka każdemu z nich?
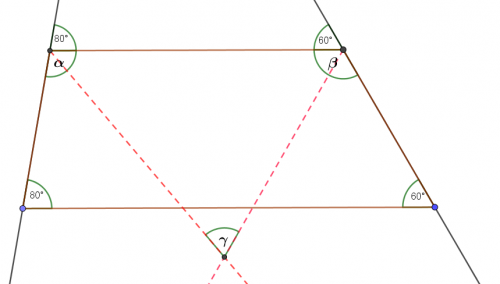
Zad. 3. W trapezie kąty przy jednej z podstaw mają miary α=80° i β=60°. Oblicz miarę kąta ostrego, pod którym przecinają się dwusieczne dwóch pozostałych kątów tego trapezu.
W maju punkty zdobyli:
- 3 – Martyna Burnos SP 3 Głogów, Zofia Chodacka SP Kotla, Natalia Czurejno SP Wykroty, Maja Dałek SP 44 Wrocław, Mateusz Galik SP Arka Wrocław, Igor Gawrzoł, SP Aslan Głogów, Rafał Frankowski SP 139 Warszawa, Julia Kałużny SP 3 Głogów, Aleksandra Koziej SP Jarczew, Wiktor Kuczaj SP 7 Nowa Ruda, Aleksander Masztalski SP 3 Mikołów, Joanna Nowakowska SP 3 Głogów, Krzysztof Pajek SP 50 Wrocław, Wiktoria Pietrzak SP 3 Głogów, Adrian Przygodzki SP Strzelce, Gabriela Pułecka SP 2 Brzeg Dolny, Oliwia Ryndak SP 26 Kraków, Oliwia Stańczyk SP Aslan Głogów, Tytus Szczapa SP Młody Kopernik Wałbrzych, Anastasia Yakovleva SP 3 Mogilno;
- 2 – Maciej Piasecki SP Tyniec Mały, Arkadiusz Piwowarczyk SP 14 Ostrowiec Świętokrzyski, Oliwia Raszewska SP 6 Boguszów-Gorce, Szymon Ryś SP 16 Wrocław, Dominika Wojdacz SP 11 Inowrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Ponieważ w każdej paczce była inna liczba czekolad, więc jedyną parą liczb ze zbioru {1, 2, 3, 4, 5, 6}, których suma wynosi 10 jest 4 i 6. Paczki Bartka zawierały po 4 i 6 czekolad.
Zad. 2. Niech t będzie czasem, po którym spotkali się turyści na trasie. Pierwszy turysta przebył drogę długości t.v1, a drugi t.v2, gdzie v1 i v2 są prędkościami z jakimi poruszali się odpowiednio pierwszy i drugi turysta. Mamy wówczas t.v1 = 21/4.v2 i t.v2 = 4.v1. Mnożąc stronami otrzymujemy równanie t2.v1.v2=9.v1.v2. Zatem t2=9, a stąd t=3. Pierwszy turysta wędrował 7 godzin, a drugi 51/4.
Zad. 3.
Po przedłużeniu ramion trapezu (patrz rysunek nizej) otrzymujemy dwa kąty odpowiadające równe kątom przy podstawie. Zatem suma kątów leżących przy każdym z ramion wynosi 180o, a stąd kąty α i β przy podstawie górnej wynoszą 100o i 120o. Dwusieczne dzielą te kąty odpowiednio na kąty po 50o i 60o Kąt γ, pod którym przecinają się dwusieczne wynosi 180o-(60o+50o)=70o.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
