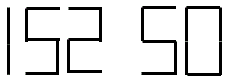
Zad. 1. W hali obsługi klientów banku Swiss Dream obowiązuje system numerków, pobieranych przy wejsciu na sale. Elektroniczny wyświetlacz na bieżąco zawiadamia, do którego stanowiska ma podejść dany klient, np. 12 143 oznacza wezwanie klienta z numerkiem 143 do okienka 12. Tomek czekał na swoją kolejkę, siedząc tyłem do wyświetlacza, ale widział go w lustrze. Jednak lustro zawieszone było wysoko, więc Tomek dla wygody obserwował jego odbicie na marmurowej posadzce. Podszedł do okienka, gdy na posadzce ujrzał poniższy napis. Jaki numerek miał Tomek i które stanowisko go obsługiwało?
Zad. 2. Uczniowie IIa otrzymali z poprawy pracy klasowej oceny 2, 3, 4 i 5. Dwój, trój i piątek było tyle samo, a czwórek było więcej niż wszystkich pozostałych ocen. Więcej niż trójkę otrzymało mniej niż 10 uczniów. Ilu uczniów otrzymało trójkę, jeśli poprawę pisało nie mniej niż 12 osób.
Zad. 3. Czy wierzchołki ośmiokąta foremnego można ponumerować liczbami od 1 do 8 tak, aby dla dowolnych trzech kolejnych wierzchołków suma numerów była większa od 13?
W czerwcu punkty zdobyli:
• 3 – Szymon Bar PG 1 Głogówek, Jakub Dobrzański G 3 Lubin, Igor Hołowacz G Akademickie PWr, Alex Kalinowski G Dwujęzyczne Góra, Michał Piórkowski G Urszulanek Wrocław, Jan Jancewicz G Akademickie PWr, Laura Stefanowska G im. Św. Franciszka z Asyżu Legnica, Julia Mazur G Lewin Brzeski, Michał Szwej G Dwujęzyczne Chorzów i Krzysztof Palatyński G Filomata Gliwice;
• 2,5 – Karol Sadowski SG Żary, Bartłomiej Bychawski G Akademickie PWr, Mikołaj Mastaliński G Akademickie PWr;
• 2 – Krzysztof Nawrocki G Bóbrka, Tomasz Lefler ZSS Wołów i Maciej Płonka G Akademickie PWr;
• 1,5 - Julia Waleńdzik PG 1 Brzeg Dolny;
• 0,5 - Łukasz Janiak G Akademickie PWr.
Zad.1. Odbiciem lustrzanym cyfry 2 jest cyfra 5 i na odwrót a cyfry zero i jeden przechodzą na siebie. Jeżeli na posadzce jest napis 152 50 to w lustrze 125 20 . Zatem na wyświetlaczu jest 05 251. Tomek miał 251 numerek a obsługiwało go stanowisko 5.
Zad. 2. Niech: x – liczba trójek (dwójek, piątek), y – liczba czwórek. Na podstawie warunków zadania otrzymujemy: y > 3x i x + y < 10 i 3x + y ≥ 12. Liczba x > 1, bo w przeciwnym wypadku y > 9 i y ≤ 9 wykluczają się. Z pierwszego i trzeciego równania wynika, że y > 3x ≥ 12 – y, zatem y > 6. Warunki x >1, y > 6 i x + y <10 spełniają liczby x = 2 i y = 7. Zatem dwóch uczniów otrzymało trójkę.
Zad. 3. Mamy osiem kolejnych trójek numerów wierzchołków trójkąta. Suma każdej trójki ma wynosić co najmniej 14. Suma wszystkich trójek powinna zatem wynosić co najmniej 112, bo 8 . 14 = 112. Tworząc trójki każdą z liczb używamy trzykrotnie, zatem ich suma wynosi: 3 . (1 + 2 + 3 + ... + 8) = 3 . 36 = 108. Otrzymujemy 108 < 112, z czego wynika, że nie można wierzchołków ośmiokąta foremnego ponumerować liczbami 1, 2, 3, ..., 8 tak, aby dla dowolnych trzech kolejnych wierzchołków suma ich numerów była większa od 13.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
Szkoda, że wyniki nie są
Szkoda, że wyniki nie są uaktualniane na bieżąco. Moi uczniowie stracili motywację do ich rozwiązania, ponieważ nie mają informacji zwrotnej, czy poprzednie zadania robili dobrze. Nie mogą nawet pokazać nauczycielowi swoich wyników, bo oceny już prawie wystawione. Duży minus dla organizatora konkursu za zniechęcenie uczniów do udziału.