Przed miesiącem mówiliśmy o zmiennych losowych, ich dystrybuancie i gęstości. Tym razem powiemy o niezależności zmiennych losowych. Pojęcie to zajmuje ważne miejsce w rachunku prawdopodobieństwa i jest wręcz kluczowe dla rozważań statystycznych.
Będziemy mówili, że zmienne losowe X i Y są niezależne, gdy dla dowolnego zdarzenia A dotyczącego zmiennej losowej X i dowolnego zdarzania B dotyczącego zmiennej losowej Y prawdopodobieństwo tego, że jednocześnie zachodzą zdarzenia A i B, jest iloczynem prawdopodobieństw tych zdarzeń tzn. P(A i B) = P(A)·P(B).
Pojęcie niezależności zmiennych losowych służy do oddania naszej intuicji o sytuacjach, w których wartość jednej zmiennej losowej nie ma wpływu na wartość drugiej zmiennej losowej. W szczególności sytuacja taka ma miejsce, gdy zmiennym losowym przypisujemy wartości, powtarzając ten sam eksperyment w tych samych warunkach (np. wielokrotnie rzucamy monetą czy kostką do gry).
Przykład 1. Eksperyment polega na dwukrotnym rzucie monetą. Rozważmy dwie zmienne losowe X i Y. Niech X przyjmuje wartość 1, gdy w pierwszym rzucie wypadł orzeł, i 0, gdy w pierwszym rzucie wypadła reszka. Z kolei niech Y przyjmuje wartość 1, gdy w drugim rzucie wypadł orzeł, i 0, gdy w drugim rzucie wypadła reszka. Wyniki obu rzutów nie są ze sobą powiązane, a zatem zmienne losowe X i Y są niezależne. Zakładamy ponadto, że moneta jest symetryczna tzn. prawdopodobieństwo wypadnięcia orła jak i wypadnięcia reszki w każdym z rzutów wynosi ½. Oznacza to, że P(X=1) = P(X=0) = P(Y=1) = P(Y=0) = ½.
Zastanówmy się nad prawdopodobieństwem zdarzenia polegającego na tym, że X=1 i Y=1. Z niezależności zmiennych losowych X i Y wynika, że P(X=1 i Y=1) = P(X=1)·P(Y=1) = ½·½ = ¼.
Nietrudno jest zauważyć, że możliwe wyniki rzutu dwiema monetami to: dwie reszki, reszka na pierwszej monecie i orzeł na drugiej monecie, orzeł na pierwszej monecie i reszka na drugiej monecie oraz dwa orły. Prawdopodobieństwo każdego z tych zdarzeń wynosi ¼. W takim razie P(X=1 i Y=1) = ¼, co zgadza się z wcześniej uzyskanym wynikiem.
Niezależność zmiennych losowych można wyrazić w języku dystrybuant. Możemy powiedzieć, że zmienne losowe X i Y są niezależne, gdy dla każdych dwóch liczb s i t mamy P(X≤s i Y≤t) = P(X≤s)·P(Y≤t), co zgodnie z definicją dystrybuanty można zapisać jako P(X≤s i Y≤t) = FX(s)·FY(t), jeśli poprzez FX i FY oznaczymy dystrybuanty zmiennych losowych X i Y.
Pojęcie niezależności zmiennych losowych uogólnia się na więcej niż dwie zmienne losowe. Mówimy, że zmienne losowe [tex]X_1, X_2, \dots, X_k[/tex] są niezależne, gdy dla dowolnych zdarzeń [tex]A_1, A_2, \dots, A_k[/tex] takich że zdarzenie [tex]A_i[/tex] dotyczy zmiennej losowej [tex]X_i[/tex], zachodzi [tex]P(A_1 \ \text{i} \ A_2 \ \text{i} \ \dots \ \text{i} \ A_k)=P(A_1)\cdot P(A_2)\cdot \dots \cdot P(A_k)[/tex]. Jeśli zaś przez [tex]F_{X_i}[/tex] oznaczymy dystrybuantę zmiennej losowej [tex]X_i[/tex], to możemy powiedzieć, że zmienne losowe [tex]X_1, X_2, \dots, X_k[/tex] są niezależne, gdy dla dowolnych liczb [tex]t_1, t_2,\dots,t_k[/tex] zachodzi [tex]P(X_1\leq t_1 \ \text{i} \ X_2\leq t_2 \ \text{i} \ \dots \ \text{i} \ X_k\leq t_k)=[/tex][tex]=F_{X_1}(t_1) \cdot F_{X_2}(t_2)\cdot \dots \cdot F_{X_k}(t_k)[/tex].
Do definicji niezależności zmiennych losowych dodamy jeszcze jedną. Powiemy, że zmienne losowe X i Y mają taki sam rozkład, jeśli mają takie same dystrybuanty (ewentualnie również takie same gęstości, jeśli te zmienne losowe mają gęstości).
Potrzebna będzie nam jeszcze jedna własność prawdopodobieństwa. Jeśli mamy dwa zdarzenia, które nie mogą zachodzić jednocześnie, ale zawsze zachodzi jedno z nich, to suma ich prawdopodobieństw wynosi 1. O takich zdarzeniach mówimy, że są to zdarzenia dopełniające się. Dla przykładu jeśli mamy daną zmienną losową X, to P(X≤1)+P(X>1) = 1. W takim razie P(X>1) = 1-P(X≤1).
Aby lepiej zrozumieć pojęcie niezależności zmiennych losowych, zastanowimy się, jak wygląda dystrybuanta maksimum i minimum zmiennych losowych. W tym celu posłużymy się prostymi przykładami.
Pierwszym z nich będzie równoległe połączenie żarówek w obwodzie elektrycznym. Wyobraźmy sobie sytuację, w której dwie żarówki są umieszczone w obwodzie elektrycznym jak na rysunku (¤ oznacza żarówkę a strzałka zwrot prądu w obwodzie):
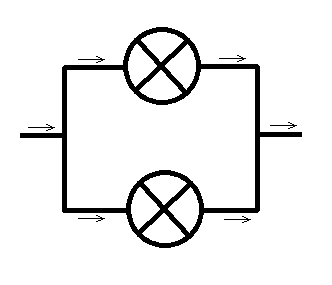
Przy takim podłączeniu żarówek przepalenie jednej żarówki nie sprawi, że druga żarówka zgaśnie, bo nawet przy przepaleniu jednej przez drugą będzie płynął prąd. Dopiero przepalenie obu spowoduje, że żadna nie będzie świecić. Jeśli czas pracy (to znaczy: czas do zgaśnięcia) żarówki pierwszej oznaczymy jako X a czas pracy drugiej żarówki jako Y, to możemy powiedzieć, że czas pracy całego układu (tzn. czas, w którym przynajmniej jedna żarówka świeci) jest równy max(X,Y) (czyli większej spośród wartości X i Y). Załóżmy, że czasy pracy poszczególnych żarówek są niezależnymi zmiennymi losowymi. Oznaczmy przez FX, FY i Fmax(X,Y) dystrybuanty zmiennych losowych X, Y i max(X,Y). Wówczas
Fmax(X,Y)(t) = P(max(X,Y)≤t) = P(X≤t i Y≤t) = P(X≤t)·P(Y≤t) = FX(t)·FY(t).
Gdybyśmy dodatkowo założyli, że zmienne losowe X i Y mają taki sam rozkład (czyli FX = FY), to wówczas okazałoby się, że Fmax(X,Y)(t) = (FX(t))2.
Inaczej sytuacja wygląda, gdy żarówki połączymy szeregowo. Schemat takiego połączenia jest przedstawiony na rysunku:
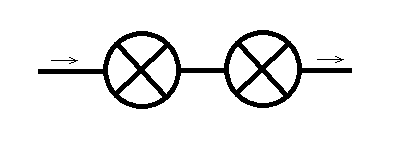
Jeśli któraś z żarówek się przepali, druga także przestanie świecić (choć niekoniecznie będzie przepalona), gdyż prąd nie popłynie przez przepaloną, a więc nie popłynie także przez drugą. Żarówki zgasną zatem w momencie przepalenia się którejkolwiek z żarówek. W takim razie czas pracy całego układu będzie wynosił min(X,Y). Jeśli przez Fmin(X,Y) oznaczymy dystrybuantę zmiennej losowej min(X,Y), to
Fmin(X,Y)(t) = P(min(X,Y)≤t) = 1- P(min(X,Y)>t) = 1- P(X>t i Y>t) = 1-P(X>t)·P(Y>t) = 1-(1-P(X≤t))·(1-P(Y≤t)) = 1-(1-FX(t))·(1-FY(t)).
Jeśli zmienne losowe X i Y mają taki sam rozkład (czyli FX = FY), to wówczas Fmin(X,Y)(t) = 1-(1-FX(t))2.
Przykład 2. Wróćmy jeszcze do przykładu podanego w miniwykładzie z października, w którym pasażer czekał na tramwaj jednej z dwóch linii i chciał pojechać tym, który szybciej przyjedzie. Jeśli czas oczekiwania na tramwaj jednej linii jest zmienną losową X a czas oczekiwania na tramwaj drugiej linii - zmienną losową Y, to czas oczekiwania na tramwaj, który szybciej przyjedzie, wynosi min(X,Y).
Mamy:
[tex]F_X(t)=F_Y(t)=\left\{\begin{array}{c,l}0,& t<0\\ \frac{t}{20},& t\in[0,20]\\ 1,& t>20\end{array},\right.[/tex]
(jak to było powiedziane w przykładzie zawartym w miniwykładzie z listopada). W takim razie
[tex]F_{\min(X,Y)}(t)=\left\{\begin{array}{c,l}1-(1-0)^2,& t<0\\ 1-(1-\frac{t}{20})^2,& t\in[0,20]\\ 1-(1-1)^2,& t>20\end{array}\right.=\left\{\begin{array}{c,l}0,& t<0\\ 1-(1-\frac{t}{20})^2,& t\in[0,20]\\ 1,& t>20\end{array}\right. .[/tex]
W przykładzie należało obliczyć, jakie jest prawdopodobieństwo, że najbliższy tramwaj przyjedzie w ciągu najbliższych 5 minut tzn. P(min(X,Y)≤5). Prawdopodobieństwo to wynosi Fmin(X,Y)(5) = 1-(1-5/20)2 = 7/16 (co zgadza się z wcześniej podanym wynikiem).
Zad 1. Mamy dane dwie zmienne losowe X i Y takie że
[tex]F_X(t)=F_Y(t)=\left\{\begin{array}{cl}1-(\frac{1}{2})^t, & t\geq 0\\ 0, &t<0\end{array}\right. .[/tex]
Ile wynosi prawdopodobieństwo, że min(X,Y)>2? Ile wynosi prawdopodobieństwo, że max(X,Y)>2?
Zad 2. Rozważamy połączenie żarówek w obwodzie elektrycznym jak na rysunku:
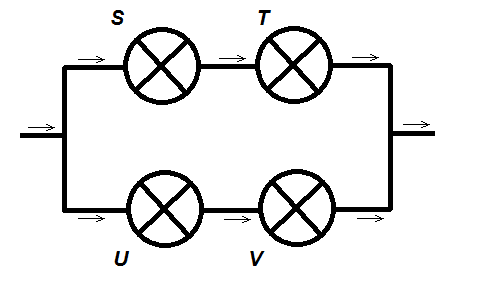
Jeśli przez FS, FT, FU i FV oznaczymy dystrybuanty czasów pracy poszczególnych żarówek (zgodnie z oznaczeniem z rysunku), to jak wyraża się dystrybuanta czasu pracy całego układu?
Wskazówka: zastanów się najpierw, jak wyraża się czas pracy systemu złożonego tylko z żarówek o czasach pracy S i T oraz systemu złożonego tylko z żarówek o czasach pracy U i V.
Zad 3. Rzucamy dwukrotnie monetą, przy której prawdopodobieństwo wyrzucenia orła wynosi ½. Niech X przyjmuje wartość 1, gdy w pierwszym rzucie wypadł orzeł, i 0, gdy w pierwszym rzucie wypadła reszka. Z kolei niech Y przyjmuje wartość 1, gdy w drugim rzucie wypadł orzeł, i 0, gdy w drugim rzucie wypadła reszka. Oblicz, korzystając z dystrybuant zmiennych losowych X i Y (nie zaś tak jak w pierwszym przykładzie z tego miniwykładu), ile wynosi prawdopodobieństwo, że X=0 i Y=0 oraz że X=1 i Y=1.
Zad 1. Dane są dwie zmienne losowe X i Y takie że dla dowolnych liczb s i t
[tex]P(X\leq s \ \text{i} \ Y\leq t)=\left\{\begin{array}{cl}1-\left(\frac{1}{2}\right)^s-\left(\frac{1}{2}\right)^t+\left(\frac{1}{2}\right)^{s+t}, & s\geq 0 \ \text{i} \ t\geq 0 \\ 0, & s<0 \ \text{lub} \ t<0\end{array}\right. .[/tex]
Czy zmienne losowe X i Y są niezależne?
Zad 2. Uogólnij podane wzory na dystrybuantę minimum i maksimum dwóch niezależnych zmiennych losowych, wyprowadzając wzory na dystrybuanty zmiennych losowych min(X1,X2,...,Xn) i max(X1,X2,...,Xn) w zależności od dystrybuant niezależnych zmiennych losowych X1,X2,...,Xn.
Zad 3. Pokaż, że dla niezależnych zmiennych losowych X i Y o tej samej dystrybuancie F i dla każdego t zachodzą nierówności: Fmax(X,Y)(t) ≤ F(t) ≤ Fmin(X,Y)(t). Uwaga: zadanie to wymaga umiejętności rozwiązania nierówności kwadratowej.
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Joanna Lisiowska | 1 | 0,5 | 0,5 | 2 |
Klasyfikacja generalna:
Joanna Lisiowska (Katolicki Zespół Edukacyjny im. Piotr Skargi w Warszawie) - 6 punktów
Adam Stachelek (Szkoła Podstawowa nr 301 w Warszawie) - 5 punktów
Jakub Ptak (Szkoła Podstawowa nr 64 we Wrocławiu) - 2 punkty
Dawid Konieczko (Społeczne Gimnazjum z Oddziałami Dwujęzycznymi w Szprotawie) - 0 punktów
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Suma |
| Daria Bumażnik | 0 | 1 | 1 | 2 |
| Tomasz Stempniak | 0,5 | 1 | 1 | 2,5 |
Klasyfikacja generalna:
Tomasz Stempniak (I Liceum Ogólnokształcące w Ostrowie Wielkopolskim ) - 7,5 punktu
Daria Bumażnik (II Liceum Ogólnokształcące im. C. K. Norwida w Jeleniej Górze) - 5 punktów
Witold Barcz (Zespół Szkół Elektryczno-Mechanicznych w Nowym Sączu) - 1 punkt
Zad. 1. Dystrybuanta zmiennej losowej min(X,Y) ma postać:
[tex]F_{\min(X,Y)}(t)=1-(1-F_X(t))\cdot
(1-F_Y(t))=\left\{\begin{array}{cl} 1- \left(\frac{1}{2}\right)^{2t},
& t\geq 0 \\ 0,& t<0\end{array}\right.[/tex].
natomiast dystrybuanta zmiennej losowej max(X,Y) ma postać:
[tex]F_{\max(X,Y)}(t)=F_X(t)\cdot F_Y(t)=\left\{\begin{array}{cl}
\left[1- \left(\frac{1}{2}\right)^t \right]^2, & t\geq 0 \\ 0,&
t<0\end{array}\right.[/tex],
W takim razie
[tex]P(\min(X,Y)>2)=1-P(\min(X,Y)\leq 2)=[/tex]
[tex]=1-F_{\min(X,Y)}(2)=\left(\frac{1}{2}\right)^{2\cdot 2}=\frac{1}{16}[/tex].
zaś
[tex]P(\max(X,Y)>2)=1-P(\max(X,Y)\leq 2)=[/tex]
[tex]=1-F_{\max(X,Y)}(2)=1-\left[1- \left(\frac{1}{2}\right)^2 \right]^2=\frac{7}{16}[/tex]
Zad. 2. Dystrybuanta czasu życia układu złożonego z żarówek o czasach pracy S i T (połączenie szeregowe) ma postać 1-(1-FS(t))·(1-FT(t)). Podobnie dystrybuanta czasu życia układu złożonego z żarówek o czasach pracy U i V (także połączenie szeregowe) ma postać 1-(1-FU(t))·(1-FV(t)). Oba te układy są połączone równolegle, a zatem dystrybuanta czasu pracy całego układu jest równa [1-(1-FS(t))·(1-FT(t))]·[1-(1-FU(t))·(1-FV(t))].
Zad. 3. Zmienne losowe X i Y mają taką samą dystrybuantę, która jest postaci:
[tex]F_X(t)=F_Y(t)=\left\{\begin{array}{c,l}0,& t<0\\ \frac{1}{2},& t\in[0,1)\\ 1,& t\geq 1\end{array}.\right.[/tex]
(patrz: przykład 2 z miniwykładu z listopada). Wobe tego dystrybuanty zmiennych losowych max(X,Y) i min(X,Y) mają postaci odpowiednio:
[tex]F_{\max(X,Y)}(t)=F_X(t)\cdot F_Y(t)=\left\{\begin{array}{c,l}0,& t<0\\ \frac{1}{4},& t\in[0,1)\\ 1,& t\geq 1\end{array}.\right.[/tex]
i
[tex]F_{\min(X,Y)}(t)=1-(1-F_X(t))\cdot
(1-F_Y(t))=\left\{\begin{array}{c,l}0,& t<0\\ \frac{3}{4},& t\in[0,1)\\ 1,& t\geq 1\end{array}.\right.[/tex]
W takim razie
[tex]P(X=0 \text{ i } Y=0)=P(\max(X,Y)=0)=[/tex]
[tex]=P(\max(X,Y)\leq 0)=F_{\max(X,Y)}(0)=\frac{1}{4}[/tex]
i
[tex]P(X=1 \text{ i } Y=1)=P(\min(X,Y)=1)=1-P(\min(X,Y)<1)=[/tex]
[tex]=1-P(\min(X,Y)\leq 0)=1-F_{\min(X,Y)}(0)=1-\frac{3}{4}=\frac{1}{4}[/tex].
Zad. 1. Zauważmy, że
[tex]P(X\leq s \ \text{i} \ Y\leq
t)=\left\{\begin{array}{cl}\left[1-\left(\frac{1}{2}\right)^s\right]\cdot \left[1-\left(\frac{1}{2}\right)^t\right],
& s\geq 0 \ \text{i} \ t\geq 0 \\ 0, & s<0 \ \text{lub} \
t<0\end{array}\right. .[/tex]
Jeśli zatem
[tex]F_X(s)=\left\{\begin{array}{cl}1-(\frac{1}{2})^s,
& s\geq 0\\ 0, & s<0\end{array}\right. [/tex] i [tex]F_Y(t)=\left\{\begin{array}{cl}1-(\frac{1}{2})^t,
& t\geq 0\\ 0, & t<0\end{array}\right. [/tex],
to P(X≤s i Y≤t) = FX(s)·FY(t), czyli zmienne losowe X i Y są niezależne.
Zad. 2. Niech [tex]F_{X_1}, F_{X_2}, \dots, F_{X_n}[/tex] oznaczają dystrybuanty niezależnych zmiennych losowych X1,X2,...,Xn. Niech Fmin(X1,X2,...,Xn) i Fmax(X1,X2,...,Xn) oznaczają dystrybuanty zmiennych losowych min(X1,X2,...,Xn) i max(X1,X2,...,Xn) odpowiednio. Wówczas
[tex]F_{\min(X_1,X_2,\dots,X_n)}(t)=P(\min(X_1,X_2,\dots,X_n)\leq t)=[/tex]
[tex]=1-P(\min(X_1,X_2,\dots,X_n)> t)=[/tex]
[tex]=1-P(X_1> t\text{ i }X_2> t\text{ i }\dots \text{ i } X_n> t)=[/tex]
[tex]=1-P(X_1> t)\cdot P(X_2> t)\cdot\dots\cdot P(X_n> t)=[/tex]
[tex]=1-[1-P(X_1\leq t)]\cdot [1-P(X_2\leq t)]\cdot\dots\cdot [1-P(X_n\leq t)=[/tex]
[tex]=1-[1-F_{X_1}(t)]\cdot [1-F_{X_2}(t)]\cdot \dots\cdot [1-F_{X_n}(t)][/tex]
i
[tex]F_{\max(X_1,X_2,\dots,X_n)}(t)=P(\max(X_1,X_2,\dots,X_n)\leq
t)=[/tex]
[tex]=P(X_1\leq t, X_2\leq t, \dots ,
X_n\leq t)=[/tex]
[tex]=P(X_1\leq t)\cdot P(X_2\leq t)\cdot\dots\cdot P(X_n\leq
t)=[/tex]
[tex]=F_{X_1}(t)\cdot F_{X_2}(t)\cdot \dots \cdot F_{X_n}(t) [/tex].
(zamieniając prawdopodobieństwo części wspólnej zdarzeń nailoczym prawdopodobieństw, korzystamy z niezależności zmiennych losowych X1,X2,...,Xn).
Zad. 3. Wiemy, że Fmin(X,Y)(t) = 1-(1-F(t))2 i Fmax(X,Y)(t) = (F(t))2. Należy zatem wykazać, że (F(t))2 ≤ F(t) ≤ 1-(1-F(t))2 dla dowolnego t. Niech x = F(t). Wówczas x∈[0,1]. Należy zatem wykazać, że x2 ≤ x ≤ 1-(1-x)2. Musimy zatem rozważyć dwie nierówności.
10 x2 ≤ x dla x∈[0,1], co po uporządkowaniu daje x2-x ≤ 0, czyli x(x-1) ≤ 0. Szkic wykresu pozwala nam się zorientować, że nierówność zachodzi.
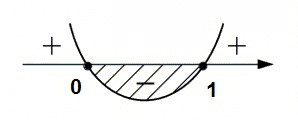
20 x ≤ 1-(1-x)2 dla x∈[0,1], co po uporządkowaniu daje ponownie x2-x ≤ 0, czyli x(x-1) ≤ 0. Szkic wykresu pozwala nam się zorientować, że nierówność zachodzi




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
