Zad. 1. Wykaż, że w dowolnym trójkącie stosunek najkrótszej wysokości do najkrótszej dwusiecznej jest większy niż √2/2.
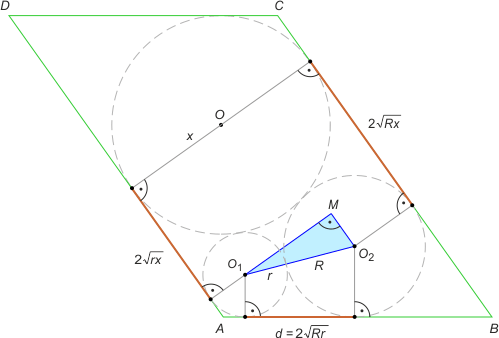
Zad. 2. Dany jest równoległobok ABCD i trzy okręgi parami zewnętrznie styczne, z których jeden jest styczny do boków AB i BC, drugi do AB i AD, a trzeci do BC i AD. Oblicz promień trzeciego okręgu, wiedząc, że odległość punktów styczności na boku AB wynosi d.
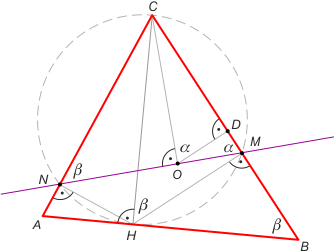
Zad. 3. Niech M i N będą rzutami prostokątnymi spodka wysokości na boki trójkąta. Wykaż, że jeśli środek okręgu opisanego leży na odcinku MN, to odcinek ten dzieli trójkąt na części o równych polach.
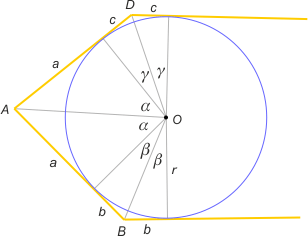
Zad. 4. (wolna amerykanka) W czworokąt ABCD wpisano okrąg o promieniu r. Punkt styczności dzieli bok AB na odcinki a i b, a bok AD na odcinki a i c. W jakich granicach może zmieniać się r?
Za zadania 1-3 punkty uzyskali:
- 30 pkt. - Dominik Bysiewicz (uczeń I LO Krosno ), Michel Migas (student PW) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 10 pkt. - Iwona Gruszecka (nauczycielka matematyki, CLV LO Warszawa).
Za zadanie 4 punkty uzyskali:
- 10 pkt. - Michel Migas,
- 2 pkt. - Dominik Bysiewicz i Tadeusz Porzucek.
Gratulacje!
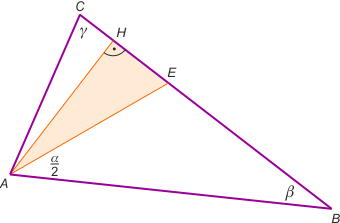
Zad. 1. Niech kąt α w trójkącie ABC będzie największy. Wówczas spodki najkrótszej wysokości i najkrótszej dwusiecznej leżą na najdłuższym boku trójkąta, czyli na BC (patrz zad. 3 z października 2018). Zauważmy, że |∡EAH| < 45°, bo w przeciwnym razie |∡AEH| = β +α/2 ≤ 45°, a tym samym 2β + α ≤ 90°, co oznaczałoby, że γ ≥ 90°, a to jest sprzeczne z założeniem. W trójkącie prostokątnym AEH mamy |AH|/|AE| > √2/2, bo równość zachodziłaby dla kąta 45°, a gdy kąt EAH maleje, to dwusieczna AE też maleje i ułamek rośnie. W przypadku |AC| > |AB| rozumujemy analogicznie.
Zad. 2. W rozwiązaniu wykorzystamy łatwy do udowodnienia fakt, że jeśli dwa okręgi o promieniach r i R są styczne zewnętrznie, to odległość s punktów styczności tych okręgów ze wspólną styczną zewnętrzną jest równa podwojonej średniej geometrycznej promieni tych okręgów, zachodzi bowiem s = (R+r)2 – (R–r)2. Niech O2M będzie równoległy do BC. Wówczas trójkąt prostokątny O1O2M ma boki o długościach |O1O2| = R+r, |O2M| = 2√Rx–2√rx oraz |O1M| = 2x–r–R. Stosując do niego twierdzenie Pitagorasa, otrzymujemy x = d.
Zad. 3. Zauważmy, ze na czworokącie NHMC można opisać okrąg. Stąd |∡CNM| = |∡CHM| = β oraz |∡CMN| = |∡CHN| = α. Niech D będzie środkiem boku BC. Wówczas |∡COD| = α (jako połowa kąta środkowego COB). Oznacza to, że kąty ACH i OCM mają równe miary. Z cechy kkk podobne są parami trójkąty ABC i NMC oraz AHC i COM. Zauważmy, że CO jest wysokością w trójkącie NMC. Stosunek pól figur podobnych równy jest kwadratowi skali podobieństwa, otrzymujemy więc z jednej strony SNMC/SABC = (CH/2 / OC)2 - stosunek promieni okręgów opisanych, a z drugiej SNMC/SABC = (OC/CH)2. Mnożąc te równości stronami, otrzymujemy (SNMC/SABC)2 = 1/4, a stąd wynika teza.
Zad. 4. (wolna amerykanka) Długość r zależy od odległości d wierzchołka C do punktu styczności z okręgiem. Gdy ta odległość maleje, czworokąt w granicznym położeniu redukuje się do trójkąta o bokach długości a+c, a+b i b+c i wówczas promień okręgu wpisanego w ten trójkąt wynosi r = S/p, gdzie S oznacza pole, a p - połowę obwodu trójkąta. Stosując wzór Herona, otrzymujemy r = √(abc/a+b+c). W przypadku gdy odległość d rośnie, graniczne położenie ilustruje rysunek (przeciwległe styczne są równoległe, a wierzchołek C znika w nieskończoności). Zauważmy, że wtedy α+β+γ = 90°, a stąd tg(α+β) = ctgγ. Otrzymujemy zatem równanie (a/r + b/r) / (1–a/r·b/r) = r/c, skąd po przekształceniach otrzymujemy r = √(ab+ac+bc). Ostatecznie √(abc/a+b+c) < r < √(ab+ac+bc).