Zad. 1. W trójkącie ABC, w którym |AB|≠|AC|, poprowadzono środkową AD. Oblicz miarę kąta BAC, wiedząc, że |∡DAC| + |∡ABC| = 90°.
Zad. 2. W czworokącie wypukłym ABCD punkty M i N są odpowiednio środkami boków AB i CD. Pola trójkątów ABN i CDM są równe, a pole ich wspólnej części jest k razy mniejsze od pola każdego z nich. Oblicz stosunek długości boków BC i AD.
Zad. 3. Wewnątrz n-kąta wypukłego (n>4) dane są dwa punkty. Wykaż, że spośród wierzchołków wielokąta da się wybrać cztery tak, by otrzymany czworokąt zawierał te punkty w swoim wnętrzu.
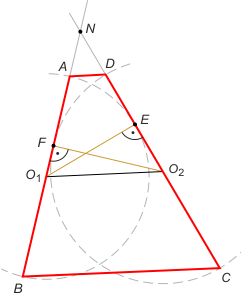
Zad. 4. (wolna amerykanka) W wypukłym czworokącie ABCD o nierównoległych bokach AB i CD prosta CD jest styczna do okręgu o średnicy AB. Wykaż, że prosta AB jest styczna do okręgu o średnicy CD wtedy i tylko wtedy, gdy proste BC i AD są równoległe.
Za zadania 1-3 punkty uzyskali:
- 30 pkt. - Michel Migas (student PW) oraz Tadeusz Porzucek (emerytowany nauczyciel, Gostyń),
- 20 pkt. - Dominik Bysiewicz (uczeń I LO Krosno ),
- 10 pkt. - Iwona Gruszecka (nauczycielka matematyki, CLV LO Warszawa).
Za zadanie 4 po 10 pkt. uzyskali: Michel Migas oraz Tadeusz Porzucek.
Gratulacje!
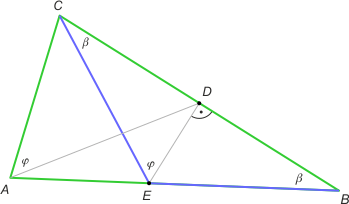
Zad. 1. Niech |AB|>|AC|, |∡DAC|=φ i |∡ABC|= β. Zachodzi φ+β = 90°. Niech punkt E leży w przecięciu symetralnej boku BC z AB. Wówczas |EC|=|EB| i kąt CDE jest prosty. Oznacza to, że |∡CED| = φ i na czworokącie AEDC można opisać okrąg (twierdzenie odwrotne do twierdzenia o kątach wpisanych opartych na tym samym łuku). Stąd kąt BAC jest prosty (warunek równoważny wpisania czworokąta w okrąg).
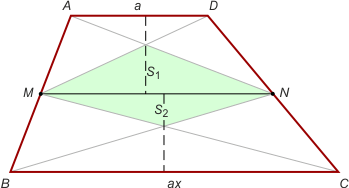
Zad. 2. Z równości pól trójkątów ABN i CMD wynika równość pól trójkątów BMN i MCN, bo MN jest środkową w pierwszych trójkątach. Oznacza to, że BC i MN są równoległe i analogicznie równoległe są AD i MN. Zatem czworokąt ABCD jest trapezem o podstawach AD i BC. Oznaczając przez h wysokość trapezu, otrzymujemy S1 = ah(x+1)2/8(x+3) oraz S2 = ah(x+1)2/8(3x+1), skąd S1 + S2 = [ah(x+1)3]/[2(x+3)(3x+1)]. Dalej rozwiązując równanie k(S1+S2) = 1/2SABCD, otrzymujemy x = (5–2k ± 2√(4–2k))/(2k–3).
Zad. 3. Niech prosta przechodząca przez wybrane punkty przecina boki AB i CD wielokąta. Wówczas A, B, C i D są szukanymi wierzchołkami. Jeśli prosta przecina bok AB i przechodzi przez wierzchołek C, to do A, B, C dodajemy dowolny wierzchołek jako D. Jeśli prosta przechodzi przez wierzchołki A i B, to nie są one kolejne i wtedy do A i B dodajemy dowolny wierzchołek leżący między A i B jako C oraz dowolny leżący między B i A (idąc po obwodzie w tym samym kierunku, co poprzednio) jako D.
Zad. 4. Niech proste AB i CD przecinają się w N oraz niech F będzie takim punktem na AB, że O2F jest prostopadłe do AB. Zauważmy, że |O1E| = |O1A| oraz |O2F| = |O2D| jako promienie odpowiednich okręgów. Oznaczmy przez α i β miary kątów odpowiednio O1O2N i O2O1N. Warunek, że prosta AB jest styczna do okręgu o środku O2, jest równoważny proporcji |O2F|:|O2D| = |O1E|:|O1A| lub |O1A|:|O2D| = |O2F|:|O1E|. Mamy |O1E| = |O1O2|sinα oraz |O2F| = |O1O2|sinβ. Stąd |O1A|:|O2D| = sinα/sinβ. Z drugiej strony z twierdzenia sinusów w trójkącie O1O2N mamy sinα/sinβ = |O1N|:|O2N|, skąd otrzymujemy |O1A|:|O2D| = |O1N|:|O2N|, co oznacza równoległość O1O2 i AD, a także BC.