Zad. 1. Którędy poprowadzić przez tarczę zegara linię prostą, tak by suma numerów godzin po jednej i po drugiej jej stronie były takie same?
Zad. 2. Rozpatrzmy 1001 liczb:
1,
1+2,
1+2+3,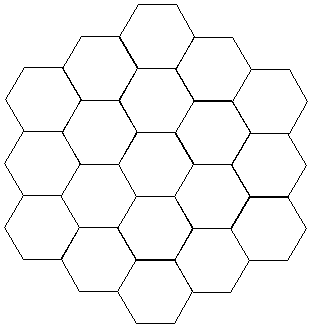
1+2+3+4,
...
1+2+3+...+999,
1+2+3+...+1000,
1+2+3+...+1001.
Ile z nich jest parzystych?
Zad. 3. Plastry miodu zbudowane są z sześciokątnych komórek. Na rysunku przedstawiono sześciokątny plaster o "boku" długości 3 takich komórek. Składa się on z 19 komórek. Z ilu komórek składałby sie taki plaster o boku 10 komórek?
Poprawne rozwiązania wszystkich zadań kwietniowych nadesłali:
Marek Kaczmarczyk z SP 3 w Ścinawie, Kacper Kadys z SP 107 we Wrocławiu, Łukasz Kajdan z SP 82 w Poznaniu, Lilla Łomnicka z SP 3 w Ścinawie, Karol Mazurek z SP w Skokach, Michał Radwański z Poznańskiej Ogólnokształcącej Szkoły Muzycznej I stopnia nr 1, Aleksandra Samol z SP w Skokach, Jadwiga Słowik z SP 34 w Gdyni, Bartłomiej Szymański z SP w Skokach, Marcin Witkowski z SP 107 we Wrocławiu, Zbigniew Zabłocki z SP 3 w Ścinawie.
Gratulujemy!
W klasyfikacji ogólnej prowadzą (na 21 możliwych punktów):
Jadwiga Słowik z SP 34 w Gdyni (19 pkt.), Łukasz Kajdan z SP 82 w Poznaniu (19 pkt.), Marek Kaczmarczyk z SP 3 w Ścinawie (18 pkt.), Lilla Łomnicka z SP 3 w Ścinawie (17 pkt.), Anna Zarobnik z SP 3 w Ścinawie (14 pkt.), Weronika Feliszek z SP 3 w Ścinawie (13 pkt.), Rafał Andrachiewicz z SP 3 w Ścinawie (12 pkt.), Marcin Cichuta z SP 3 w Ścinawie (11 pkt.).
Zad. 1. Pogrupujmy wszystkie numery godzin do łatwiejszego sumowania: 1+12 + 2+11 + 3+10 + 4+9 + 5+8 + 6+7 = 6·13, zatem po każdej stronie prowadzonej prostej ich suma ma wynosić 3·13 = 39, a że trzy pierwsze pary (1 i 12, 2 i 11, 3 i 10) znajdują się w górnej połowie tarczy, można je po prostu oddzielić. Inaczej podzielić się nie da, bo liczba 12:
- nie może być po jednej stronie z dziewiątką (wówczas byłoby tam co najmniej 12+11+10+9=42),
- jeśli jest z dziesiątką, mamy rozwiązanie opisane powyżej,
- jeśli z lewej strony tarczy ma być tylko z jedenastką, z prawej nie da się dobrać numerów, tak by suma ich wszystkich wyniosła 39,
- podobnie jeśli do 12 należałoby dodawać tylko liczby z prawej połowy tarczy.
Zad. 2. Dane liczby to kolejno 1, 3, 6, 10, 15, ... Zauważmy, że pierwsza z nich jest nieparzysta, następna jest większa o liczbę parzystą, czyli też nieparzysta, kolejna większa o nieparzystą, czyli parzysta, następna większa o parzystą, czyli też parzysta, następna z kolei jest o nieparzystą większa od ostatniej parzystej i potem sytuacja się powtarza. Kolejno mamy więc: niep., niep., parz., parz., niep., niep., parz., parz. itd. Cykl powtarza się co 4 liczby, czyli do tysiąca składników dokładnie połowa liczb jest parzysta, a potem dochodzi jedna nieparzysta z nowego cyklu. Odpowiedź to zatem 500.
Zad. 3. Zauważmy, że plaster opisany w zadaniu można uzyskać, zaczynając od pojedynczej komórki miodu i dokładając komórki wokół niej, potem wokół powstałej w ten sposób pierwszej warstwy itd., aż warstw będzie 9. W kolejnych warstwach dokładamy 6 komórek, 12, 24 itd. (zawsze umieszczamy je "pomiędzy" każdymi dwiema z poprzedniej warstwy).
W rezultacie będzie ich więc 1+6+6·2+6·3+...+6·9 = 1+6·(1+2+3+...+9) = 1+6·45 = 271.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
