Zad. 1. Waga z rysunku może być jednoznacznie opisana symbolem (-3 (-1 1) (1 1)) (2 3).
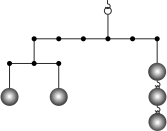
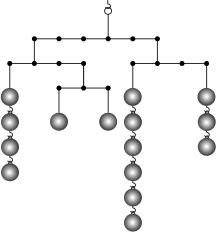
Naszkicuj wagę opisaną symbolem (-3 (-1 4) (2 (-1 1) (1 1))) (2 (-1 6) (2 3)).
Zad. 2. Przyjrzyj się kolejnym wielokrotnościom liczby 142 857. Dlaczego to bardzo szczególna liczba? Jak dalece działa jej magia? Znajdź inną liczbę o podobnej własności.
Zad. 3. Przeanalizuj poniższą definicję funkcji f .
FUNCTION f(n, k)
IF n<k THEN f=n ELSE f = f(INT(n/k), k) + f(n–k*INT(n/k), k)
END FUNCTION
Podaj wartości: f(15, 2), f(16, 2), f(89, 10), f(2012, 10), f(99, 3), f(100, 3).
W kwietniu zawodnicy zdobyli następujące liczby punktów:
- 3 - Krzysztof Danielak (student informatyki przemysłowej na PWr), Krystyna Lisiowska (redaktor z Warszawy), Marzena Wąsiewicz (informatyk, a obecnie gospodyni domowa z Kajetan)
- 2,75 - Wojciech Tomiczek (inżynier z Lipowej), Daria Bumażnik (uczennica II LO W Jeleniej Górze)
- 2,5 - Piotr Wróbel (inżynier sprzedaży z Brwinowa)
- 1,5 - Andrzej Piasecki (administrator IT z Oleśnicy)
- 1 - Dominik Zygmunt (student bankowości i finansów cyfrowych na UŁ).
Po siedmiu miesiącach trwania Ligi prowadzą:
- Marzena Wąsiewicz (20,75 pkt)
- Piotr Wróbel (19,25 pkt)
- Wojciech Tomiczek (18,75 pkt)
- Andrzej Piasecki (17,75 pkt)
- Krystyna Lisiowska (17,25 pkt)
- Krzysztof Danielak (16,75 pkt)
- Daria Bumażnik (13,5 pkt)
- Dominik Zygmynt (12 pkt)
Gratulujemy!
Zad. 1. Rozwiązanie przedstawia rysunek.
Zad. 2. Zadanie pochodzi z tomiku Cicer cum caule, czyli groch z kapustą Juliana Tuwima, w którym osobny rozdział stanowią rozmaite matematyczne łamigłówki i magiomatematyczne właściwości. Rzeczywiście ciąg początkowych wielokrotności liczby 142 857 wygląda bardzo interesująco:
142 857 · 2 = 285714
142 857 · 3 = 428571
142 857 · 4 = 571428
142 857 · 5 = 714285
142 857 · 6 = 857142.
Każdy z tych wyników jest przestawieniem cyfr pierwszego czynnika z zachowaniem ich porządku cyklicznego (jakby liczba zapętlona była w kółko, dlatego takie liczby nazywamy kolistymi). W kolejnym iloczynie magia przestaje działać, bo 142 857 · 7 = 999 999.
Wykonując dalsze próby, zauważamy jednak, że 142 857 · 8 = 1 142 856. Wystarczy pierwszą cyfrę tej liczby dodać do ostatniej i magia powraca, dostajemy znowu 142 857. Postępując podobnie z różnymi innymi mnożnikami, otrzymujemy liczby zapisane tymi samymi cyframi i w tym samym porządku z dodatkową grupą cyfr z przodu, które na końcu dodajemy, wracając do wyjściowej liczby kolistej, np.
142 857 · 9 = 1 285 713 i 285 713 + 1 = 285 714
142 857 · 10 = 1 428 570 i 428 570 + 1 = 428 571
142 857 · 89 = 12 714 273 i 714 273 + 12 = 714 285.
Wyjątki stanowią wyniki mnożenia przez wielokrotności siódemki. Po wykonaniu opisanych operacji dostajemy wtedy liczby zapisane samymi dziewiątkami, np.
142 857 · 14 = 1 999 998 i 999 998 + 1 = 999 999
142 857 · 84 = 11 999 988 i 999 988 + 11 = 999 999.
Podobne własności (liczby kolistej) ma każda liczba stanowiąca okres podstawowy ułamka 1/p (gdzie p jest pierwsze), który ma p–1 cyfr, tzn. p jest różne od 2 i 5, a najmniejsza liczba złożona z samych dziewiątek podzielna przez p ma p-1-cyfr (istnienie takiej liczby wynika z małego twierdzenia Fermata). Na przykład liczba 142 857 jest okresem ułamka dla p=7. Kolejna liczba to p=17, dla której otrzymujemy okres 16-cyfrowy i kolistą liczbę 5 882 352 941 176 470. Mamy 882 352 941 176 470 · 2 = 11 764 705 882 352 940 i
1 764 705 882 352 940 + 1 = 1 764 705 882 352 941.
Kolejna liczbę kolistą znajdziemy dla p=19.
Zad. 3. Funkcja podaje (zapisaną dziesiętnie) sumę cyfr pierwszej liczby w systemie o podstawie będącej drugą liczbą. Mamy:
f(15, 2) = (1111)2 = 4
f(16, 2) = (10000)2 = 1
f(89, 10) = (89)10 = 17
f(2012, 10) = (2012)10 = 5
f(99, 3) = (10200)3 = 3
f(100, 3) = (10201)3 = 4.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
