Zad. 1. 777 robaczków usiadło po jednym w wierzchołkach 2000-kąta foremnego. Pajęczyca Tekla oznaczyła każdy z boków tego wielokąta liczbami 0, 1 lub -1, według następujących reguł:
- bok, na którego obu końcach siedzą robaczki, oznaczony jest jako 1,
- bok, na którego żadnym końcu robaczek nie siedzi, oznaczony jest jako -1,
- pozostałe boki są oznaczone jako 0.
Jaka jest suma liczb użytych przez Teklę?
Zad. 2. Chmara pewnego gatunku szarańczy może liczyć nawet 50 miliardów owadów. Każdy z nich zjada dziennie 2 gramy zboża. Ile ton zboża może zjeść takie stado w ciągu doby? Ilu ludzi można by tym zbożem wyżywić w ciągu roku? Podaj wielkości przyjęte do obliczeń.
Zad. 3. Na kalkulatorze prostym dodano klawisz "cos". Jak za pomocą takiego kalkulatora rozwiązać równanie cosx = x, używając jak najmniej różnych klawiszy? Ile razy wystarczy nacisnąć te klawisze, aby podać pierwiastki z dokładnością do dwóch miejsc po przecinku?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Jadwiga Bąk (nauczycielka z Karłowic), Andrzej Piasecki (administrator IT z Oleśnicy), Marzena Wąsiewicz (gospodyni domowa z Kajetan),
- 2,5 pkt. - Krzysztof Danielak (student informatyki przemysłowej na PWr), Szymon Meyer (student matematyki na PWr), Dawid Migacz I LO Tarnów, Wojciech Tomiczek (inżynier z Lipowej),
- 2 pkt. - Mikołaj Bilski SP 6 Jelenia Góra,
- 1,75 pkt. - Krystyna Lisiowska (redaktor z Warszawy),
- 1,5 pkt. - Daria Bumażnik (studentka chemii i toksykologii sądowej na UWr).
Po siedmiu miesiącach trwania Ligi w czołówce znajdują się:
- 23,5 pkt. - Marzena Wąsiewicz
- 22,75 pkt. - Jadwiga Bąk
- 22,5 pkt. - Andrzej Piasecki
- 21 pkt. - Szymon Meyer
- 19,1 pkt - Jakub Ptak
- 18,75 pkt. - Krzysztof Danielak
- 18,5 pkt - Mikołaj Bilski
- 17,75 pkt. - Wojciech Tomiczek
- 17,25 pkt. - Krystyna Lisiowska
- 16 pkt. - Dawid Migacz
- 15,75 pkt. - Daria Bumażnik.
Zad. 1. -2000+2·777 = -446
Zad. 2. Stado szarańczy zjada w ciągu doby 100 000 ton zboża. Do przeżycia człowiek potrzebuje minimum 1 000 kcal dziennie. Wartość kaloryczna 100 g pieczywa to 260 kcal. Przyjmijmy, że zboże daje z tego 250 kcal, więc aby dostarczyć organizmowi 1000 kcal trzeba spożyć 400 g zboża dziennie, czyli 146 kg rocznie. Zboża zjedzonego w ciągu jednego dnia przez szarańczę wystaczyłoby więc maksymalnie do nakarmienia przez rok prawie 700 000 ludzi (100 000 000 : 146 = 684 931), czyli wszystkich mieszkańców Wrocławia. Jeśli w rozwiązaniu nie podano, w jaki sposób ustalono spożycie roczne/dzienne, przyznawano 0,5 pkt.
Zad. 3. Wystarczy wpisać dowolną liczbę (lub nawet zacząć od zera, które pojawia się na ekranie po włączeniu kalkulatora), a następnie wielokrotnie naciskać klawisz "cos". Oblicza się w ten sposób jedyny pierwiastek równania cosx = x, tzw. metodą iteracyjną.
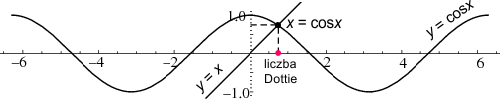
Otrzymana wartość liczbowa zależy od tego, czy rachunki na kalkulatorze ustawione są w stopniach, czy radianach. Dla stopni otrzymujemy 0,999847741..., a dla radianów 0,739085133..., przy czym w tym drugim przypadku ciąg jest znacznie wolniej zbieżny. Dla uzyskania dokładności dwóch miejsc po przecinku w stopniach wystarczy na ogół jedno naciśnięcie klawisza "cos", a w radianach potrzeba ich 4-10 (w zależności od wybranej wartości początkowej).
Otrzymana w ten sposób liczba jest granicą ciagu zdefiniowanego rekurencyjnie jako:
a1 = c, an+1 = cos an
i nazywana jest liczbą Dottie. Nazwę tę wprowadził w 2007 amerykański matematyk Samuel Kaplan na łamach Mathematics Magazine. Kiedy jeszcze chodził do szkoły, jego nauczycielka francuskiego (o imieniu Dottie) zauważyła ze zdziwieniem, że kiedy wpisuje do kalkulatora dowolną liczbę, a potem wielokrotnie naciska klawisz "cos", wyniki zawsze są zbieżne do tej samej liczby. Zapytała o to męża - nauczyciela matematyki - który wyjaśnił jej, że ogląda zbieżność ciągu do swojej granicy. A dlaczego ta granica nie zależy od wyboru pierwszego wyrazu ciągu? I dlaczego liczba Dottie zdefiniowana powyżej jako granica ciągu jest jednocześnie pierwiastkiem równania cosx = x? Jeśli powyższy ciąg jest zbieżny, to istnieje liczba g równa [tex]\lim_{n\to\infty}a_n[/tex]. Wówczas przechodząc obustronnie do granicy w równości an+1 = cos an i korzystając z ciągłości funkcji kosinus (co powoduje, że możemy wejść z granicą podznak tej funkcji), otrzymujemy:[TEX] \lim\limits_{n\to\infty}a_{n+1} = \lim\limits_{n\to\infty}\cos(a_n)[/TEX] [TEX]\lim\limits_{n\to\infty}a_{n+1} = \cos(\lim\limits_{n\to\infty}a_n) ,[/TEX]zatem otrzymujemy g = cos g, co chcieliśmy wykazać.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
