Zad. 1. Ile rozwiązań ma poniższy rebus? (z okazji 25-lecia Kangura Matematycznego w Polsce)
Zad. 2. Ile liczb naturalnych mniejszych od 2016 ma więcej dzielników niż liczba 2016?
Zad. 3. Na kalkulatorze graficznym lub w programie komputerowym ryusującym wykresy równań parametrycznych zbadaj kształty linii
x(t) = sin (t)
y(t) = cos (kt/2), gdzie t[tex]\in[/tex]R.
Dla jakich całkowitych dodatnich k narysowane linie przechodzą przez punkt (0, 0)?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Jadwiga Bąk (nauczycielka z Karłowic), Daria Bumażnik (studentka chemii i toksykologii sądowej na UWr), Krzysztof Danielak (student informatyki przemysłowej na PWr), Andrzej Piasecki (administrator IT z Oleśnicy), Wojciech Tomiczek (inżynier z Lipowej), Marzena Wąsiewicz (gospodyni domowa z Kajetan),
- 2 pkt. - Krystyna Lisiowska (redaktor z Warszawy), Szymon Meyer (student matematyki na PWr),
- 1 pkt. - Jakub Ptak SP 64 Wrocław.
Po ośmiu miesiącach trwania Ligi w czołówce znajdują się:
- 26,5 pkt. - Marzena Wąsiewicz
- 25,75 pkt. - Jadwiga Bąk
- 25,5 pkt. - Andrzej Piasecki
- 23 pkt. - Szymon Meyer
- 21,75 pkt. - Krzysztof Danielak
- 20,75 pkt. - Wojciech Tomiczek
- 20,1 pkt. - Jakub Ptak
- 19,25 pkt. - Krystyna Lisiowska
- 18,75 pkt. - Daria Bumażnik
- 18,5 pkt. - Mikołaj Bilski
- 16 pkt. - Dawid Migacz.
Zad. 1. Jest jedno rozwiązanie: 10 580 – 922 = 9 658.
Zad. 2. Liczba 1680 < 2016 ma rozkład na czynniki pierwsze 24·3·5·7, więc liczba jej dzielników wynosi 5·2·2·2 = 40 (dwójkę można wziąc do dzielnika z dowolną potęgą od 0 do 4, pozostałe czynniki pierwsze albo w potędze 0, albo 1). Natomiast liczba 2016 =25·32·7, ma 6·3·2 = 36 dzielników. Jest to jedyne rozwiązanie.
Zad. 3. Otrzymane linie są przykładami krzywych Lissajoux. Przechodzą przez (0, 0) dla k nieparzystych.
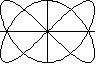
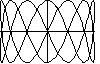
k=1 k=3 k=5 k=7
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
