Zad. 1. Znajdź wszystkie liczby całkowite k, które spełniają nierówność [tex] \frac{1}{2+\frac{3}{4+\frac{5}{6}}} <\frac{1}{k}<\frac{6}{5+\frac{4}{3+\frac{2}{1}}}. [/tex]
Zad. 2. Lena ma wyciąć z kartki o wymiarach 30 cm na 40 cm siatkę czworościanu foremnego. Jaką powinna obrać długość krawędzi, aby czworościan ten miał możliwie największą objętość?
Zad. 3. Szkoła, do której uczęszcza Nadia, liczy mniej niż 1000 uczniów. Można ich podzielić na 11 równolicznych grup. Natomiast gdy podzielimy ich na 7 równolicznych grup, to zostanie 1 osoba, a jeżeli podzielimy ich na 13 równolicznych grup, to zostanie 6 osób. Ilu uczniów liczy szkoła Nadii?
W kwietniu punkty zdobyli:
- 3 – SP Alicja Picińska 64 Wrocław, Gabriela Pułecka SP 2 Brzeg Dolny;
- 2 – Eliza Banaszkiewicz, Anna Frankowska SP 139 Warszawa, Antoni Grębowiec SP 44 Wrocław, Aleksander Masztalski SP 3 Mikołów, Szymon Michalik SP 3 Przymierza Rodzin Warszawa, Ewa Nowakowska SP Strzelce, Karolina Piątkowska SP 16 Wrocław, Yaraslau Sialiuk SP 82 Wrocław, Julia Strzelecka SP 50 Wrocław, Milena Żaczek SP Jedlnia Letnisko;
- 1 – Nadia Dymkowska SP 50 Wrocław, Krzysztof Pajek SP 50 Wrocław, Aleksandra Pniaczek SP 50 Wrocław, Barbara Podoba SP Tomaszów Lubelski, Krzysztof Świta SP ?, Ignacy Włodarski SP 36 Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. [tex] \frac{1}{2+\frac{3}{4+\frac{5}{6}}} =\frac{29}{76} [/tex] oraz [tex] \frac{6}{5+\frac{4}{3+\frac{2}{1}}} =\frac{30}{29} [/tex]. Zatem [tex] \frac{29}{76}< \frac{1}{k} <\frac{30}{29} [/tex], czyli [tex] \frac{29}{76}< \frac{1}{k} <2\frac{18}{29} [/tex]. Jedynymi liczbami całkowitymi spełniającymi tę nierówność są 1 i 2.
Zad. 2. Oznaczmy długość krawędzi czworościanu przez a. Zauważmy, że siatka czworościanu może być trójkątem równobocznym o boku długości 2a lub równoległobokiem o kącie ostrym 60° i bokach długości a i 2a.
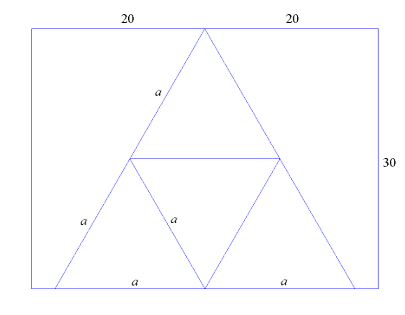
W pierwszym przypadku podstawa największego trójkąta równobocznego mieszczącego się na kartce o wymiarach 30 cm × 40 cm będzie leżała na boku o długości 40 cm, a jego wysokość będzie równa 30 cm. Ze wzoru na wysokość trójkąta równobocznego otrzymujemy [tex] \frac{2a\sqrt{3}}{2}=30 [/tex], skąd [tex]a=10\sqrt{3} [/tex] cm.
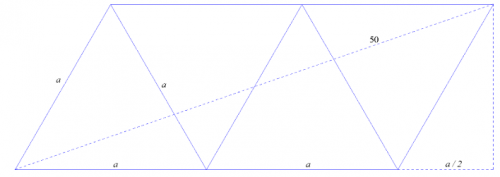
W drugim przypadku dłuższa przekątna największego równoległoboku o kącie ostrym 60° i bokach długości a i 2a mieszczącego się na kartce o wymiarach 30 cm × 40 cm będzie pokrywać się z przekątną prostokąta. Z twierdzenia Pitagorasa wynika, że jej długość to 50 cm. Zatem poszukujemy długości mniejszego boku równoległoboku o bokach długości a i 2a oraz kącie ostrym 60° i przekątnej długości 50 cm. Z twierdzenia Pitagorasa mamy [tex] (\frac{5a}{2})^2+ (\frac{a\sqrt{3}}{2})^2=50^2 [/tex], skąd [tex] a=\frac{50\sqrt{7}}{7} [/tex]. Ponieważ [tex] \frac{50\sqrt{7}}{7}>10\sqrt{3} [/tex], czworościan będzie miał największą objętość, gdy [tex] a=\frac{50\sqrt{7}}{7} [/tex].
Zad. 3. Niech x oznacza liczbę uczniów w szkole Nadii. Z warunków zadania wynika, że istnieją liczby naturalne k i l takie, że x = 7k+1 oraz x = 13l+6. Najmniejsza wspólna wielokrotność liczb 13 i 7 to 91. Przekształcając równania, otrzymujemy 13x = 91k+13 i 7x = 91l+42. Przekształcając dalej drugie równanie, mamy układ 13x = 91k+13 i 14x = 2·91l+84. Odejmując stronami od drugiego pierwsze równanie, mamy x = 91(2l−k)+71. Dzieląc liczbę uczniów przez 91, otrzymujemy resztę 71. Liczba uczniów może być więc równa: 71, 162, 253, 344, 435, 526, 617, 708, 799, 890 albo 981. Spośród nich liczbą spełniającą wszystkie warunki zadania (podzielność przez 11) jest 253.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
