Zad. 1. Czy można kwotę 400 złotych wypłacić za pomocą 20 monet o wartościach 5 zł, 20 zł, 50 zł tak, aby znalazła się wśród nich przynajmniej jedna moneta każdego rodzaju? Jeśli da się wypłacić, podaj na ile sposobów. Jeśli nie, krótko uzasadnij.
Zad. 2. Znajdź liczbę dwucyfrową, która wzrasta o 20%, gdy odwrócimy kolejność jej cyfr.
Zad. 3. Trójkąt równoboczny i sześciokąt foremny mają równe obwody. Jaki jest stosunek pola trójkąta do pola sześciokąta?
W maju punkty zdobyli:
• 3 – Eliza Banaszkiewicz SP Strzelce, Anna Frankowska SP 139 Warszawa, Antoni Grębowiec SP 44 Wrocław, Szymon Michalik SP 3 Przymierza Rodzin Warszawa, Ewa Nowakowska SP Strzelce, Karolina Piątkowska SP 16 Wrocław, SP Alicja Picińska 64 Wrocław, Adrian Pniaczek SP Strzelce, Gabriela Pułecka SP 2 Brzeg Dolny, Yaraslau Sialiuk SP 82 Wrocław, Julia Strzelecka SP 50 Wrocław;
• 2,5 – Nadia Dymkowska SP 50 Wrocław,
• 2 – Aleksander Masztalski SP 3 Mikołów, Hanna Zawadzka SP Jedlnia-Letnisko;
• 1 – Barbara Podoba SP Tomaszów Lubelski, Ignacy Włodarski SP 36 Wrocław, Milena Żaczek SP Jedlnia Letnisko.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech x oznacza liczbę monet 5-złotowych, y – liczbę monet 20-złotowych, a z - liczbę monet 50-złotowych. Zbadamy, czy układ równań x+y+z = 20 i 5x+20y+50z = 400 ma rozwiązanie w zbiorze trójek liczb naturalnych. Wyznaczając x z pierwszego równania i podstawiając do drugiego, otrzymujemy 5.(20–x–y)+20y+50z = 400, skąd y = 20–3z, a stąd wyznaczamy możliwe wartości y oraz z i na tej podstawie wyliczamy wartości x. Kwotę 400 zł możemy wypłacić zgodnie z warunkami zadania na 6 sposobów dla (x, y, z) równych: (2, 17, 1), (4, 14, 2), (6, 11, 3), (8, 8, 4), (10, 5, 5), (12, 2, 6).
Zad. 2. Niech a oznacza cyfrę dziesiatek, a b cyfrę jednosci szukanej liczby. Liczbę dwucyfrową możemy zapisać w postaci 10a+b. Na podstawie warunków zadania otrzymujemy 10b+a = 6/5(10a+b). Po przekształceniu tego równania otrzymujemy 44/5b = 11a, skąd 4b = 5a. Ponieważ szukana liczba ma być mniejsza od 100, zatem jedyną dobrą parą jest a=4, b=5, a wyjściowa liczba to 45.
Zad. 3. Sześciokąt ma sześć jednakowych boków, a trójkąt trzy. Ponieważ obie figury mają takie same obwody, bok sześciokąta musi być dwa razy krótszy od boku trójkąta. Sześciokąt możemy podzielić na sześć jednakowych trójkątów równobocznych, a trójkąt na cztery takie trójkąty, stąd stosunek pola trójkąta do pola sześciokąta wynosi 4/6 = 2/3.
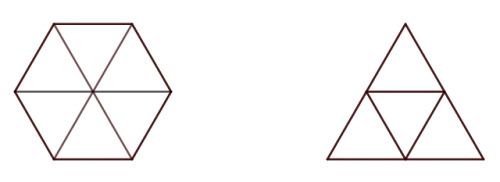
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
