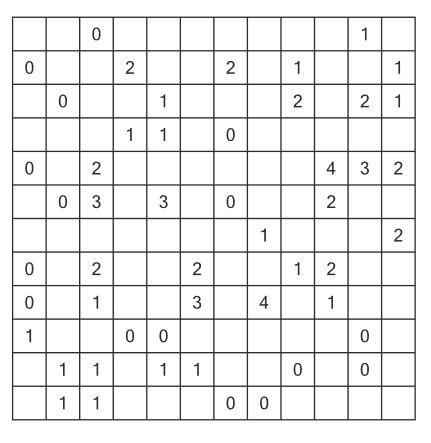
Zad. 1. Poniższy diagram przedstawia planszę łamigłówki "Statki". Na pustych polach należy rozmieścić cztery jednomasztowce, trzy dwumasztowce, dwa trzymasztowce i jeden czteromasztowiec (n-masztowiec zajmuje n kolejnych kratek w pionie lub poziomie stykających się bokami). Cyfry oznaczają, na ilu sąsiednich polach (stykających się bokiem lub rogiem z polem z cyfrą) znajdują się pola z okrętami. Okręty nie mogą się stykać ani bokiem, ani rogiem. Rozmieść statki na planszy. W rozwiązaniu prześlij skan lub zdjęcie otrzymanego rysunku.
Zad. 2. Na ekranie komputera wyświetla się wartość 2024!. Alicja i Ben grają w następującą grę: Alicja sumuje cyfry zapisanej liczby i wynik wpisuje do komputera. Wtedy Ben sumuje cyfry nowej liczby i wynik też wpisuje do komputera. Robią tak na przemian. Po pewnym czasie na ekranie pojawia się liczba jednocyfrowa. Jaka?
Zad. 3. Na płaszczyźnie rozlano dwa ogromne kubełki z farbą: czerwoną i zieloną. Farby się nie mieszały i nie nakrywały, ale pokryły całą płaszczyznę. Czy to możliwe, że zawsze znajdziemy na niej dwa jednokolorowe punkty odległe o 1? Uzasadnij odpowiedź.
W tym miesiącu punkty otrzymali:
- 3 pkt. - Daria Bumażnik - doktorantka na WCh UWr, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Tomasz Tomiczek - nauczyciel z Lipowej, Marzena Wąsiewicz - nauczycielka z Kajetan, Michał Węgrzyn - ALO PWr Wrocław,
- 2 pkt. - Agata Leśnicka - lekarz z Gdańska, Joanna Miłkowska - pracownik biurowy ze Stalowej Woli, Edward Nowicki - informatyk z Poznania,
- 1 pkt. - Kasper Przenzak - analityk ryzyka z Krakowa.
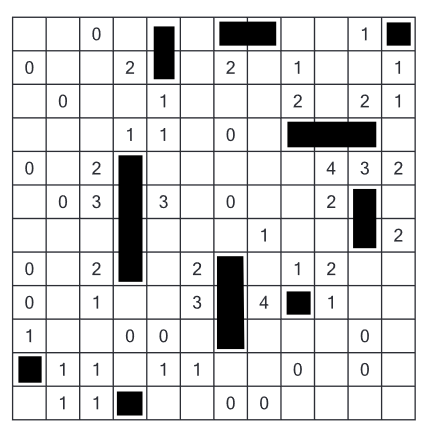
Zad. 1. Rozwiązanie przedstawia diagram.
Zad. 2. Suma cyfr dla liczb większych niż jednocyfrowe jest mniejsza niż dana liczba, zatem proces opisany w grze musi w skończenie wielu krokach prowadzić do liczby jednocyfrowej (dlaczego?). Suma cyfr liczby ma taką samą resztę z dzielenia przez 9, co sama liczba. 2024! dzieli się przez 9, a liczby jednocyfrowe, które dzielą się przez 9 to 0 i 9. Proces nigdy nie da liczby 0 (dlaczego?), zatem ostatnią liczbą otrzymaną w grze jest 9.
Zad. 3. Na pomalowanej płaszczyźnie zawsze znajdziemy dwa jednokolorowe punkty w odległości 1. Weźmy trzy wierzchołki dowolnego trójkąta równobocznego o boku długości 1. Ponieważ mamy 3 punkty, a tylko 2 kolory farby, któreś dwa wierzchołki muszą mieć ten sam kolor, c.b.d.o.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
