Zad. 1. Rozwiąż nierówność x3-4x > 7x2-28.
Zad. 2. Chorągiew husarii atakuje regiment piechoty z odległości 350 m. Przez pierwsze 50 m jadą stępem z prędkością 6 km/h, następne 150 m jadą kłusem z prędkością 12 km/h, potem przechodzą do galopu na odcinku 120 m z prędkością 25 km/h, żeby ostatecznie na 30 m przed starciem przejść do cwału z prędkością 60 km/h. Atakowani muszkieterowie nie przesuwają się, mogą oddawać salwy co 20 s (aby mieć czas na przeładowanie broni). Zasięg ich muszkietów to 250 m. Ile maksymalnie salw, które dosięgną husarzy, mogą oddać muszkieterzy przed starciem?
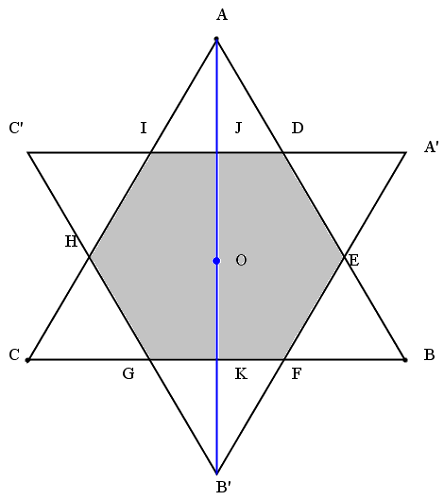
Zad. 3. Trójkąt równoboczny o boku długości 9 cm obrócono wokół środka o kąt 60o. Figura złożona z wyjściowego i obróconego trójkąta to tzw. gwiazda Dawida występująca np. na fladze Izraela. Oblicz pole wspólnej części obu trójkątów.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Aleksandra Domagała G 23 Wrocław, Oliwia Kropidłowska G 1 Wrocław, Weronika Kwiatkowska G Bądkowo, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Zofia Ogonek G 58 Warszawa, Łukasz Pawlak G Dwujęzyczne Oborniki Śląskie, Iwo Pilecki-Silva G 26 Wrocław, Mateusz Rzepecki G 14 Wrocław i Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski,
- 2,5 pkt. - Kacper Gembara G w ZSS Wołów, Magdalena Owczarek G Dwujęzyczne Legionowo, Olga Sławatyniec G Kamienna Góra i Krzysztof Żmuda G Wieczfnia Kościelna,
- 2 pkt. - Helena John G Wielowieś, Przemysław Rybarczyk G Integracyjne Stargard Szczeciński i Mateusz Winiarski G Dwujęzyczne Krosno,
- 1,5 pkt. - Patrycja Łukasik G 13 Wałbrzych, Maria Pająk G 1 Żory i Michał Pelc G 2 Wołów,
- 1 pkt. - Daniel Międzyrzecki G Miękinia,
- 0,5 pkt. - Dominik Bysiewicz G Dwijęzyczne Krosno.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu.
Zad. 1. Rozwiązaniem nierówności jest zbiór [tex]x\in(-2;2)\cup(7;+\infty)[/tex]. Nierówność możemy zapisać równoważnie jako x·(x2-4) > 7·(x2-4). Teraz rozpatrzymy dwa przypadki:
- x2-4 > 0 tj. [tex]x\in(-\infty;-2)\cup(2;+\infty)[/tex]; wtedy po podzieleniu stronami przez x2-4 otrzymamy x>7, co jest spełnione przez liczby [tex]x\in(7;+\infty)[/tex];
- x2-4 < 0 tj. [tex]x\in(-2;2)[/tex]; wtedy po podzieleniu stronami przez x2-4 otrzymamy x<7, co jest spełnione przez liczby [tex]x\in(-2;2)[/tex].
Sumując rozwiązania nierówności w obu przypadkach otrzymujemy odpowiedź.
Zad. 2. Muszkieterowie oddadzą maksymalnie 3 salwy, które dosięgną husarów. Od pierwszej salwy z odległości 250 m husaria ma do pokonania 100 m kłusem, 120 m galopem i 30 m cwałem. Po przeliczeniu prędkości na m/s, dostajemy prędkości kłusa, galopu i cwału równe odpowiednio 3,(3) m/s, 6,9(4) m/s i 16,(6) m/s. Czas, jaki zajmie husarii przejechanie 100 m kłusem, to 100/3,(3) = 30 s; 120 m galopem przejadą w 120/6,9(4) = 17,28 s, a 30 m cwałem przejadą w 30/16,(6) = 1,8 s. Łącznie zajmie im to 49,08 s. W ciągu tego czasu muszkieterowie zdążą oddać jeszcze dwie salwy.
Zad. 3. Pole części wspólnej obu trójkątów jest równe 27√3/2 cm2. Po obróceniu trójkąta równobocznego o 60° wokół jego środka otrzymamy gwiazdę sześcioramienną. Część wspólna trójkątów jest sześciokątem foremnym (jak uzasadnić jego równoboczność i równokątność?). Bok ID tego sześciokąta jest zarazem bokiem trójkąta równobocznego IOD przystającego do trójkątów IAD, IC'H oraz DA'E. Wobec tego C'I≡ID≡DA', skąd |ID|=3 (bo |C'A'|=9). Sześciokąt jest więc sumą sześciu trójkątów równobocznych o boku 3, zatem jego pole wynosi 6·9√3/4 = 27√3/2 cm2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
