Zad. 1. Jaką masę musi mieć piankowa deska pływacka, aby utrzymać na powierzchni wody pływaka o wadze 45 kg? Przyjmij, że gęstość ciała ludzkiego to 1,1 kg/dm3, a gęstość piankowej deski to 0,15 kg/dm3.
Zad. 2. Po okrągłym torze o długości 400 m poruszają się dwa samochody. Jeśli jadą w tym samym kierunku, to szybszy samochód wyprzedza wolniejszy co 10 sekund. Jeśli poruszają się w przeciwnych kierunkach, to mijają się co 4 sekundy. Oblicz szybkości obu samochodów w km/h.
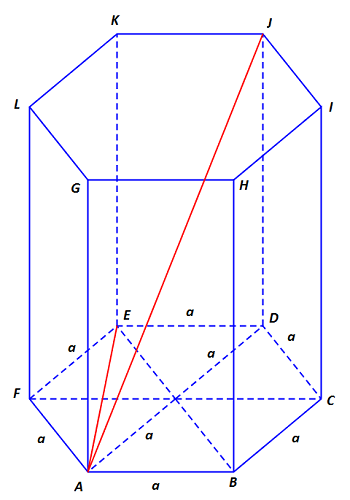
Zad. 3. Dłuższa przekątna graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy równej a jest 3 razy dłuższa od krótszej przekątnej podstawy tego graniastosłupa. Oblicz jego objętość.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kacper Gembara G w ZSS Wołów, Oliwia Kropidłowska GM 1 Wrocław, Konrad Litwiński GM 86 Warszawa, Zofia Ogonek GM 58 Warszawa, Iwo Pilecki-Silva GM 26 Wrocław, Mateusz Rzepecki GM 14 Wrocław i Michał Stempniak GM Sióstr Salezjanek Ostrów Wielkopolski,
- 2,5 pkt. - Dominik Bysiewicz GM Dwujęzyczne Krosno, Magdalena Owczarek GM Dwujęzyczne Legionowo, Krzysztof Pięta GM Grodzisk Wielkopolski, Przemysław Rybarczyk GM Integracyjne Stargard Szczeciński, Mateusz Winiarski GM Dwujęzyczne Krosno i Krzysztof Żmuda GM Wieczfnia Kościelna,
- 2 pkt. - Aleksander Glapa GM Grodzisk Wielkopolski, Helena John GM Wielowieś, Joanna Lisiowska KZE Warszawa, Weronika Schwartz GM Grodzisk Wielkopolski, Olga Sławatyniec GM Kamienna Góra i Daniel Sokulski GM 2 Olsztyn,
- 1,5 pkt. - Aleksandra Domagała GM 23 Wrocław, Marcin Oleksy GM Lewin Brzeski, Łukasz Pawlak GM Dwujęcyczne Oborniki Śląskie i Paweł Stępczyński GM Lewin Brzeski,
- 1 pkt. - Tomasz Hupental GM Złotoryja i Weronika Kwiatkowska GM Bądkowo.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Zad. 1. Masa deski pływackiej musi wynosić co najmniej 0,722 kg. Niech x oznacza szukaną masę deski. Za gęstość wody przyjmiemy 1 kg/dm3. Pływak zanurzony z deską w wodzie nie utonie, jeśli średnia gęstość jego ciała i deski będzie nie większa niż gęstość wody. Średnią gęstość ciała pływaka i deski obliczymy jako iloraz ich łącznej masy i łącznej objętości. Objętość pływaka jest równa 45/1,1, a objętość deski x/0,15. Oznacza to, że musimy rozwiązać nierówność 1≥(45+x)/(45/1,1+x/0,15). Po przekształceniach dostajemy x≥0,722 kg. Ktoś dociekliwy mógłby spytać, co by było, gdyby to nie była deska pływacka, tylko deska surfingowa. W takim przypadku pływak nie jest zanurzony w wodzie i przy obliczaniu średniej gęstości nie bierzemy pod uwagę jego objętości. Dostajemy nierówność 1≥(45+x)/(x/0,15), która po rozwiązaniu daje x≥7,941 kg.
Zad. 2. Szybkość szybszego samochodu to 252 km/h, a wolniejszego 108 km/h. Niech vs oznacza szybkość szybszego z aut, a vw wolniejszego. Gdy auta jadą w przeciwnych kierunkach, pomiędzy spotkaniami pokonują łącznie 400 m, przy czym szybsze pokonuje drogę równą vs·4, a wolniejsze vw·4. Dostajemy równanie (vs+vw)·4=400. Gdy oba auta jadą w tym samym kierunku, pomiędzy spotkaniami szybsze pokonuje drogę dłuższą o 400 m od wolniejszego. Stąd dostajemy równanie (vs-vw)·10=400. Rozwiązując układ tych dwóch równań, dostajemy vs=70 m/s i vw=30 m/s. W celu przeliczenia jednostek na km/h, wystarczy podzielić wyniki przez 1000 (bo 1 km = 1000 m) i pomnożyć przez 3600 (bo 1 godz = 3600 s), tzn. pomnożyć przez 3,6.
Zad. 3. Objętość tego graniastosłupa wynosi 3/2·a3·√69. Długość przekątnej AE jest równa podwojonej wysokości trójkąta równobocznego o boku a, czyli |AE|=a√3. Stąd długość przekątnej AJ to 3·a√3. Z twierdzenia Pitagorasa zastosowanego do trójkąta ADJ obliczamy długość krawędzi DJ będącej wysokością graniastosłupa, |DJ|=a√23. Objętość graniastosłupa to iloczyn pola jego podstawy i wysokości, czyli w naszym przypadku V = 6·1/2·a·a√3/2·a√23 = 3/2·a3·√69.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
