Tekst został napisany w oparciu o arkusz kalkulacyjny MS Excel 2013. Inne wersje Excela mogą się nieznacznie różnić od prezentowanej.
W tym miesiącu kontynuujemy poznawanie tabel przestawnych. Pierwsze kroki w ich obsłudze stawialiśmy w ubiegłym miesiącu.
W ramach tego miniwykładu będziemy się posługiwali przykładami opartymi na tym samym zbiorze danych co poprzednio tzn. na tabeli zawierającej informacje o kandydatach ubiegających się o przyjęcie na studia. Plik z danymi znajduje się tu. Zachęcamy do wykonania wszystkich opisanych czynności samodzielnie dla lepszego przyswojenia treści miniwykładu.
W zeszłym miesiącu zliczyliśmy osoby z każdego województwa. W tym celu w polu WIERSZE umieściliśmy "Województwo" (a w polu WARTOŚCI dowolna kolumnę, byleby poprzez wybór opcji "Licznik" zliczać obiekty, najwygodniej którąś z kolumn z danymi tekstowymi, np. "Imię"). Niekoniecznie musimy być zainteresowani wyświetleniem wyników dotyczących wszystkich województw. Jeśli chcemy znać liczbę kandydatów tylko z niektórych województw (np. z województwa dolnośląskiego i sąsiednich), wystarczy, że rozwiniemy nagłówek "Województwo" w tabeli przestawnej, klikając przycisk z trójkątem znajdujący się po prawej stronie pola, a następnie na liście, która się nam ukaże, odznaczymy te województwa, o których informacji nie chcemy wyświetlać.

W naszym zestawieniu czasem chcemy wziąć po uwagę tylko jednostki spełniające określony warunek. Dla przykładu: może nas interesować liczba kandydatów z podziałem na płeć i województwo, ale tylko w miastach liczących powyżej 20 000 mieszkańców. W takim wypadku będzie wygodnie, jeśli w polu WIERSZE umieścimy "Województwo", w polu KOLUMNY umieścimy "Płeć", natomiast kolumnę z dodatkową informacją, która będzie decydowała o tym, czy dana osoba będzie włączona do naszego podsumowania, czy też nie - w tym wypadku kolumnę "Pow. 20 tys." - umieścimy w nieużywanym dotąd obszarze FILTR. Nad tabelą przestawną pojawi się pole "Pow. 20 tys." z dopiskiem: (Wszystkie) i możliwością rozwinięcia. Gdy wyświetka się napis: (wszystkie), do utworzenia tabeli przestawnej brane są pod uwagę wszystkie osoby, bez względu na miejsce zamieszkania. Jeśli rozwiniemy wspomniane pole i zaznaczymy tylko "T", do utworzenia tabeli przestawnej zostaną wzięte tylko osoby z miast liczących powyżej 20 000 mieszkańców.
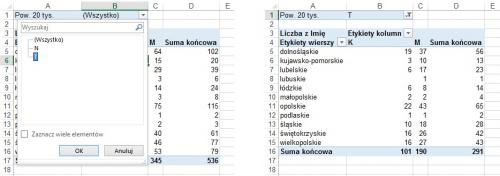
Gdybyśmy chcieli wyświetlić informacje o liczbie liczbie kandydatów z podziałem na mieszkających w miastach powyżej 20 000 mieszkańców i tych mieszkających w mniejszych miejscowościach oraz z podziałem ze względu na płeć, ale interesowałyby nas informacje tylko o określonych województwach (np. o województwie dolnośląskim i województwach sąsiednich), to w polu WIERSZE umieścimy "Płeć", w polu KOLUMNY "Pow. 20 tys." (lub na odwrót), natomiast w polu FILTR umieścimy "Województwo". W kolejnym kroku rozwiniemy pole "Województwo" powyżej tabeli przestawnej, zaznaczymy pole "Zaznacz wiele elementów", a następnie zaznaczymy interesujące nas województwa.
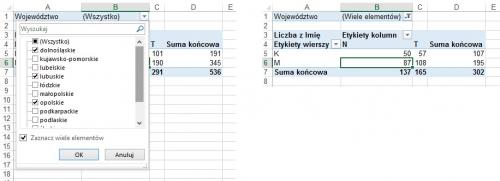
Tabele przestawne pozwalają nie tylko policzyć, ile jednostek w bazie należy do określonej grupy, ale także jaką część wszystkich jednostek stanowi dana grupa.
Wróćmy do pytania, od którego rozpoczęliśmy nasze eksperymenty z tabelami przestawnymi, tj. od pytania o to, ile w bazie było osób danej płci. Aby udzielić odpowiedzi na to pytanie skonstruowaliśmy tabelę przestawną w ten sposób, że "Płeć" była w polu WIERSZE (a w polu WARTOŚCI dowolna kolumna, byleby poprzez wybór opcji "Licznik" zliczać wiersze). Aby przekonać się o tym, jaką część wszystkich osób stanowią kobiety, a jaką mężczyźni, wchodząc w "Ustawienia pola wartości", wybieramy kartę "Pokazywanie wartości jako". Tam zamiast "Bez obliczeń" możemy wybrać "% sumy końcowej" lub "% kolumny" (bo liczby zostały wyświetlone w kolumnie). Wynik zostanie wyświetlony w procentach.
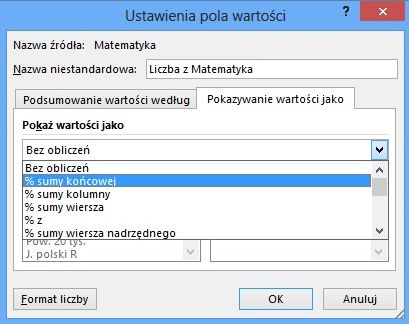
Kiedy zestawiliśmy dwie cechy, liczby osób zilustrowane w tabeli przestawnej można przedstawić zarówno jako część wszystkich liczb w wierszu bądź kolumnie, jak też jako część liczby wszystkich osób. Aby to zilustrować, spójrzmy na tabelę, w której obliczymy liczbę osób zdających podstawowy i rozszerzony egzamin z matematyki z podziałem na płeć. Uczynimy to w ten sposób, że w polu WIERSZE umieścimy "Płeć", natomiast w polu "KOLUMNA" umieścimy "Matematyka R". W polu WARTOŚCI umieszczamy jakąkolwiek kolumnę, byle użyć dla mniej opcji "Licznik". Wchodząc do karty "Ustawienia pola wartości" i dalej: "Pokazywanie wartości jako", możemy wybrać jedną z trzech opcji:
- "% sumy końcowej" pozwoli nam dowiedzieć się, jaka część wszystkich osób była kobietami i zdawała matematykę na poziomie rozszerzonym, jaka część wszystkich osób była kobietami i zdawała matematykę na poziomie podstawowym itd. W takim wypadku wszystkie liczby w tabeli powinny się sumować do 100%,
- "% sumy wiersza" pozwoli nam obliczyć, jaka część wszystkich kobiet zdawała maturę na określonym poziomie i podobnie: jaka część mężczyzn zdawała maturę na określonym poziomie. Tutaj sumy wierszy wynoszą 100%,
- "% sumy kolumny" pozwoli nam odpowiedzieć na pytanie, jaka część osób zdających matematykę na poziomie rozszerzonym była kobietami, a jaka mężczyznami, i taką samą informację pozyskać o osobach zdających matematykę na poziomie podstawowym. Teraz to kolumny sumują się do 100%.
Trzeba zwrócić uwagę, że przy wyborze opcji "% sumy końcowej", "% sumy wiersza" i "% sumy kolumny" odpowiednie stosunki są wyznaczane tylko w oparciu o informacje zawarte w tabeli przestawnej. Jeśli na przykład wyświetlamy informacje tylko o niektórych województwach, to wówczas "% sumy końcowej" będzie się odnosił tylko do kandydatów z tych województw, a nie do kandydatów z całej Polski. Odwołując się zatem do wcześniejszego przykładu, w których sprawdzaliśmy, ile jest osób określonej płci, możemy powiedzieć, że umieszczając w polu FILTR "Województwo" i wybierając tylko województwo dolnośląskie oraz województwa z nim sąsiadujące, dowiemy się np. tego, że 64,57 % kandydatów z tych województw to mężczyźni.

Na podstawie danych z arkusza kalkulacyjnego, którego dotyczą przykładu omówione w miniwykładzie, utwórz tabele przestawne, które pozwolą odpowiedzieć na następujące pytania:
Zad. 1. Jaki odsetek wszystkich kandydatów pochodzi z województwa dolnośląskiego?
Zad. 2. Jaki odsetek wszystkich kandydatów stanowią mężczyźni z województwa dolnośląskiego?
Zad. 3. Jaki odsetek kandydatów z województwa dolnośląskiego stanowią mężczyźni?
Zad. 4. Ile jest kobiet wśród kandydatów z województw: podlaskiego, lubelskiego i podkarpackiego łącznie?
Zad. 5. Jaki odsetek kandydatów z województw: podlaskiego, lubelskiego i podkarpackiego łącznie stanowią kobiety?
Zad. 6. Jaki odsetek kandydatów płci żeńskiej z województw: podlaskiego, lubelskiego i podkarpackiego łącznie zdawało maturę z matematyki na poziomie rozszerzonym?
Jako rozwiązanie prześlij odpowiedzi na powyższe pytania wraz z arkuszem kalkulacyjnym, w którym będą się znajdowały tabele przestawne, na podstawie których można udzielić odpowiedzi. Każda tabela przestawna powinna się znajdować w osobnej karcie, a karty powinny być podpisane numerami pytań. Odpowiedź na każde pytanie (wraz z potwierdzającą ją tabelą przestawną) warta jest 0,5 punktu.
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Zad. 4 | Zad. 5 | Zad. 6 | Suma |
| Jakub Ptak | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
| Adam Stachelek | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
Klasyfikacja generalna:
Jakub Ptak (Szkoła Podstawowa nr 64 we Wrocławiu) - 6 punktów
Adam Stachelek (Szkoła Podstawowa nr 301 w Warszawie) - 6 punktów
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Zad. 4 | Zad. 5 | Pyt. 6 | Suma |
| Mateusz Winiarski | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
Klasyfikacja generalna:
Mateusz Winiarski (Gimnazjum Dwujęzyczne im. Mikołaja Kopernika w Krośnie) - 6 punktów
W tym miesiącu zawodnicy osiągnęli następujące wyniki:
| Imię i nazwisko | Zad. 1 | Zad. 2 | Zad. 3 | Zad. 4 | Zad. 5 | Zad. 6 | Suma |
| Marcin Kuna | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0 | 2,5 |
| Joanna Lisiowska | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
| Wojciech Wiśniewski | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 3 |
Klasyfikacja generalna:
Joanna Lisiowska (XXI Liceum Ogólnokształcące im. H. Kołłątaja w Warszawie) - 6 punktów
Wojciech Wiśniewski (I Liceum Ogólnokształcące im. W. Kętrzyńskiego w Giżycku) - 6 punktów
Marcin Kuna (VII Liceum Ogólnokształcące im. K. K. Baczyńskiego we Wrocławiu) - 5,5 punktu
Wyniki znajdują się w tym pliku. Kolorem zielonym zaznaczono liczby, które wzięto pod uwagę przy formułowaniu odpowiedzi.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
