Zad. 1. Niech H oznacza ortocentrum (tzn. punkt przecięcia wysokości) trójkąta ostrokątnego ABC. Wykaż, że okręgi opisane na wszystkich trójkątach o wierzchołkach w punktach ze zbioru {A, B, C, H} mają jednakowe promienie.
Zad. 2. Wykaż, że iloczyn odległości ortocentrum i środka okręgu opisanego na trójkącie od dowolnego boku tego trójkąta jest stały.
Zad. 3. Niech M, N, K będą punktami styczności okręgu wpisanego w trójkąt ABC odpowiednio z bokami AB, BC i AC. Niech prosta równoległa do MN przechodząca przez środek D boku AC przecina proste AB i BC odpowiednio w punktach S i T. Wykaż, że |TC| = |KD| = |AS|.
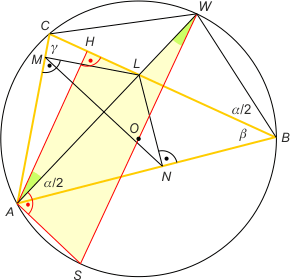
Zad. 4. (wolna amerykanka) Niech L i W będą punktami przecięcia dwusiecznej kąta A w trójkącie ABC odpowiednio z bokiem BC i okręgiem opisanym na tym trójkącie. Niech M i N będą rzutami prostokątnymi punktu L odpowiednio na boki AC i AB. Wykaż, że pole trójkąta jest równe 1/2|AW|·|MN|.
Za rozwiązania zadań 1-3 następujące liczby punktów zdobyli:
- 30 pkt. - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Włodzimierz Bąk (nauczyciel akademicki UO), Iwona Gruszecka (nauczycielka matematyki, G 42 Warszawa), Sabina Khady Sy (studentka UJ), Michel Migas (student PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Mikołaj Sikora (III LO Tarnów), Paweł Wesołowski (II LO Końskie), Robert Ciężabka (student AGH)
- 20 pkt. - Zygmunt Krawczyk (nauczyciel matematyki, SLO Żary), Szymon Janusz (I LO Kraków), Adam Wrzesiński (student UŚ).
Zadanie 4 w pełni poprawnie rozwiązali, uzyskując 10 pkt.: Jacek Bagiński, Włodzimierz Bąk, Robert Ciężabka, Sabina Khady Sy, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Michał Sikora, Wojciech Tomiczek (inżynier z Lipowej), Adam Wrzesiński.
Gratulacje!
Zad. 1. Niech O1 będzie środkiem okręgu opisanego na trójkącie ABH. Rozważmy czworokąt AO1BO. Mamy |∡AOB| = 2γ, bo to kąt środkowy w okręgu opisanym na trójkącie ABC. Stąd |∡AOM| = γ, bo prosta OM jest symetralną boku AB i osią symetrii trójkąta AOB. Zatem |∡OAB| = 90°-γ = |∡OBA|. Z drugiej strony mamy |∡AHB| = |∡FHE| = 180°-γ (suma kątów czworokąta FHEC). Wówczas |∡AO1B| = 2γ, bo jest to wypukły kąt środkowy w okręgu opisanym na trójkącie ABH. Zatem |∡O1BA| = 90°-γ = |∡O1AB|. Oznacza to, że czworokąt AO1BO jest rombem. Stąd wynika, że |OA| = |OA1|. Pozostałe przypadki rozważamy analogicznie.

Zad. 2. Rozważymy osobno przypadek trójkąta ostrokątnego i rozwartokątnego. W przypadku trójkąta prostokątnego szukany iloczyn w każdym wypadku wynosi oczywiście 0.
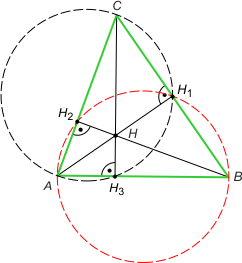
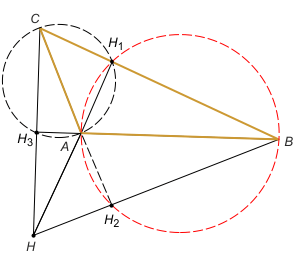
W rozwiązaniu wykorzystamy fakt (*) |AH| = 2|OM1|, |BH| = 2|OM2| i |CH| = |OM3|, gdzie O jest środkiem okręgu opisanego na trójkącie ABC, H jest ortocentrum trójkąta, a M1, M2, M3 są środkami boków odpowiednio a, b i c. Uzasadnienie tego faktu można znaleźć w zad. 3, maj 2015.
Niech H1, H2 i H3 są spodkami wysokości poprowadzonych odpowiednio z wierzchołków A, B i C. Zarówno w przypadku trójkąta ostrokątnego jak i rozwartokątnego na czworokątach AH1CH3 oraz BH1AH2 można opisać okręgi. W przypadku trójkąta ostrokątnego na mocy twierdzenia o dwóch cięciwach okręgu otrzymujemy równość |AH|·|HH1| = |CH|·|HH3| = |BH|·|HH2|. Natomiast w przypadku trójkąta rozwartokątnego ten sam rezultat otrzymujemy na mocy twierdzenia o siecznych okręgu (tzw. twierdzenie o potędze punktu względem okręgu). Podstawiając równość z faktu (*), otrzymujemy tezę.
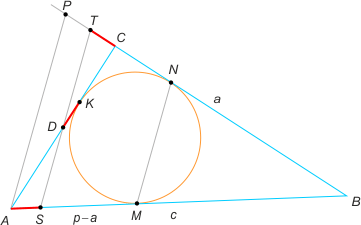
Zad. 3. Nie zmniejszając ogólności, załóżmy że c>a. Wiemy, że |AM| = |AK| = p–a, gdzie p oznacza połowę obwodu trójkąta ABC (patrz rozwiązanie zad. 2, październik 2016). Przez wierzchołek A prowadzimy prostą równoległą do MN przecinającą prostą BC w punkcie P. Z twierdzenia Talesa otrzymujemy |AS| = |PT|. Rozważamy teraz trójkąt ACP. Punkt D jest środkiem boku AC oraz DT jest równoległe do AP, zatem T jest środkiem boku PC. Stąd |AS| = |TC|. Z drugiej strony zauważamy, że |PC| = 2|TC| = |PB|–|CB| = c–a, skąd |TC| = (c–a)/2 oraz |KD| = |AK|–|AD| = |AM|–|AC|/2 = p–a–b/2 = (c–a)/2. Stąd |TC| = |DK| = |AS|. W przypadku gdy c=a mamy |AS| = |TC| = |DK| = 0.
Zad. 4. Załóżmy, że γ>β. Niech WS będzie średnicą okręgu. Wówczas |∡AWS| = 90°–|∡ASW| = 90°–|∡ABW|, bo oba są wpisane w okrąg i oparte na tym samym łuku AW. Zatem |∡AWS| = 90°–(β+α/2) = (γ–β)/2. Z drugiej strony |∡HAW| = α/2–|∡CAH| = α/2–(90°–γ) = (γ–β)/2. Oznacza to, że trójkąty prostokątne AHL i AWS są podobne. Mamy zatem |AH|/|AL| = |AW|/|WS| = |AW|/2R, czyli |AL|·|AW| = |AH|·2R (oznaczmy ten warunek *). Z kolei z twierdzenia sinusów w trójkącie AMN mamy |MN|/sinα = |AL|, bo AL jest średnicą okręgu opisanego na czworokącie ANML. Podstawiając do warunku (*), otrzymujemy (|MN|/sinα)·|AW| = |AH|·2R, czyli |MN|·|AW|/2 = |AH|·2R·sinα/2. Uwzględniając, że z twierdzenia sinusów w trójkącie ABC zachodzi 2Rsinα = |BC|, otrzymujemy tezę.