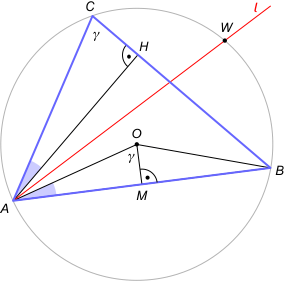
Zad. 1. Niech O oznacza środek okręgu opisanego na trójkącie ABC, a H - spodek wysokości opuszczonej na bok BC. Wykaż, że dwusieczna kąta BAC jest jednocześnie dwusieczną kąta OAH.
Zad. 2. Wykaż, że jeśli środki boków dwóch dowolnych czworokątów pokrywają się, to czworokąty te mają równe pola.
Zad. 3. Dany jest trójkąt równoramienny ABC, w którym AB≡BC. Niech E jest rzutem
prostokątnym spodka wysokości BH na bok BC. Niech M jest środkiem odcinka HE. Wykaż, że proste BM i AE są prostopadłe.
Zad. 4. (wolna amerykanka) Spośród wszystkich kwadratów, których wierzchołki leżą wewnątrz lub na brzegu sześciokąta foremnego o boku a, znajdź ten, który ma najdłuższy bok.
Za rozwiązania zadań 1-3 następujące liczby punktów zdobyli:
- 30 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Iwona Gruszecka (nauczycielka matematyki, G 42 Warszawa), Sabina Khady Sy (studentka nanotechnologii UJ), Michel Migas (student matematyki PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Mikołaj Sikora (III LO Tarnów), Paweł Wesołowski (II LO Końskie) i Robert Ciężabka (student AGH),
- 20 - Szymon Janusz (I LO Kraków) oraz Zygmunt Krawczyk (nauczyciel matematyki, SLO Żary).
W kategorii "wolnej amerykanki" punkty zdobyli:
- 10 - Jacek Bagiński, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Mikołaj Sikora, Robert Ciężabka oraz Wojciech Tomiczek (inżynier, Lipowa)
- 8 - Sabina Khady Sy
Składamy gratulacje i życzenia ciekawych rozwiązań w Nowym Roku.
Zad. 1. Wystarczy wykazać równość kątów OAM i HAC. Zauważmy, że |∡AOM| = γ, bo jest połową kąta środkowego AOB opartego na łuku AB, na którym oparty jest kąt wpisany ACB. Stąd |∡OAM| = 90°–γ. Z drugiej strony w trójkącie AHC mamy |∡HAC| = 90°–γ, co kończy dowód.
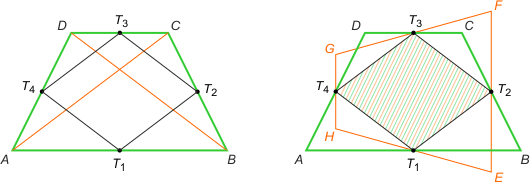
Zad. 2. Niech T1, T2, T3 i T4 oznaczają środki kolejnych boków czworokąta ABCD. Pole czworokąta T1T2T3T4 jest równe połowie pola czworokąta ABCD. Wynika to z faktu, że odcinki T1T2 i T3T4 są równoległe do przekątnej BD, a odcinki T2T3 i T4T1 do przekątnej AC (bo są liniami średnimi odpowiednich trójkątów). Zatem czworokąt T1T2T3T4 jest równoległobokiem. Ponadto długości jego boków stanowią połowy długości odpowiednich przekątnych czworokąta ABCD, zatem PAT1T4 + PT1BT2 + PT2CT3 + PT3DT4 = 1/4 PABD + 1/4 PABC + 1/4 PBCD + 1/4 PCDA = 1/2 PABCD. Zatem pola wszystkich czworokątów spełniających treść zadania równe są podwojonemu polu tego samego równoległoboku.
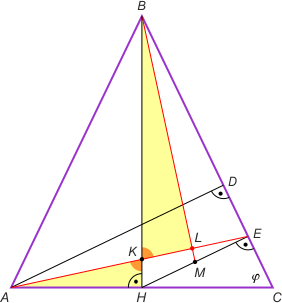
Zad. 3. Poprowadźmy wysokość trójkąta z wierzchołka A (AD || HE). Wówczas z twierdzenia Talesa E jest środkiem odcinka DC. Rozważmy trójkąty AKH (prostokątny) i BKL. Kąty AKH i BKL są przystające jako wierzchołkowe. Pokażemy, że kąty KAH i KBL też są przystające. Zauważmy, że wszystkie trójkąty prostokątne BHC, BHE, HEC i ADC są podobne na mocy cechy kkk (mają kąt prosty i kąt α). Mamy zatem |HE|/|BH| = |CD|/|AC|, czyli 2|HM|/|BH| = 2|EC|/|AC|, a to oznacza |HM|/|BH| = |EC|/|AC|, skąd wynika podobieństwo trójkątów AEC i BHM (cecha bkb). Zatem kąty EAC i HBM są przystające. Stąd wynika już podobieństwo trójkątów AKH i BKL, czyli także prostokątność BKL, co daje tezę.
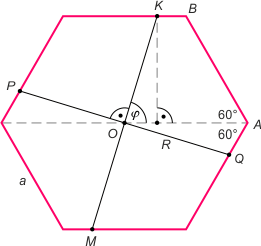
Zad. 4. (wolna amerykanka) Sześciokąt foremny i kwadrat są figurami środkowosymetrycznymi, więc największy z możliwych kwadratów powinien mieć wspólny środek symetrii O z sześciokątem. Niech K oznacza jeden z wierzchołków szukanego kwadratu, a M - punkt do niego symetryczny względem O. Niech R będzie rzutem prostokątnym punktu K na prostą OA. Punkty P i Q niech będą punktami wspólnymi brzegu sześciokąta z prostą prostopadłą do KM. Niech |∡AOK| = φ. W trójkącie prostokątnym KRO mamy |KO| = |KR|/sinφ = a√3/2sinφ. Z drugiej strony |∡QOA| = 90°–φ, skąd |∡AQO| = 30°+φ. Z twierdzenia sinusów w trójkącie OQA mamy |OQ|/sin60° = |AO|/sin(30°+φ). Uwzględniając, że |AO| = |AB| = a, mamy |OQ| = a√3/2sin(30°+φ). Aby zadanie miało rozwiązanie, powinna zachodzić nierówność |OQ|≥|KO| (bo KM jest przekątną kwadratu), czyli powinno być sin(30°+φ) ≤ sinφ (ozn. *). Zauważmy, że |∡BOA|<φ, zatem otrzymujemy zależność 60° < φ ≤ 90°. Rozwiązując nierówność (*), otrzymujemy 75° ≤ φ ≤ 90°. Wraz ze wzrostem kąta φ maleje długość przekątnej KM. Oznacza to, że należy przyjąć φ = 75°. Wówczas długość boku szukanego kwadratu wynosi √2|KO| = a(3–√3).








Pytanie
W poprzednim miesiącu użyłem jednego z rozmowań, które chcę użyć i w tym miesiącu. Czy mogę się odwołać do niego czy muszę je odtworzyć?
Odp.
Odtworzyć, chyba że występuje w rozwiązaniu firmowym. Wtedy można się na to rozwiązanie powołać. Nie przechowujemy rozwiązań z poprzednich miesięcy.