Od stycznia 2014 zadania Ligi Zadaniowej dla Gimnazjów należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Licznik ułamka to iloczyn czterech kolejnych liczb naturalnych, a mianownik jest iloczynem trzech kolejnych liczb parzystych. Udowodnij, że ułamek jest skracalny przez 24.
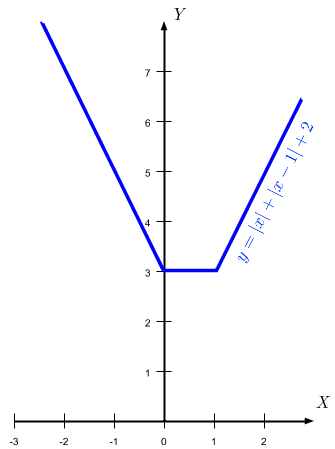
Zad. 2. Naszkicuj wykres funkcji y=|x|+|x-1|+2.
Zad. 3. W trójkąt równoboczny wpisano drugi trójkąt równoboczny tak, aby wierzchołki mniejszego trójkąta leżały na bokach większego. Jakie wartości może przyjmować stosunek pól większego do mniejszego trójkąta?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Bartosz Czyżewski GM 1 Jelenia Góra i Michał Stempniak GMSS Ostrów Wielkopolski,
- 2,5 pkt. - Joanna Lisiowska KZE Warszawa, Maciej Pająk GM 13 Wrocław, Przemysław Rybarczyk GIM Stargard Szczeciński i Wojciech Wiśniewski GM 3 Giżycko,
- 2 pkt. - Klaudia Marcinkiewicz GM 24 Katowice,
- 1,5 pkt. - Mateusz Rzepecki GM 14 Wrocław.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po pięciu miesiącach Ligi z wynikiem 15 pkt. (na 15 możliwych!) prowadzi Bartosz Czyżewski z GM 1 Jelenia Góra. Gratulujemy!
Zad. 1. Ułamek ten możemy zapisać jako $$\frac{n(n+1)(n+2)(n+3)}{2m(2m+2)(2m+4)}=\frac{n(n+1)(n+2)(n+3)}{8m(m+1)(m+2)},$$ gdzie n jest dowolną liczbą naturalną, a m dowolną liczbą całkowitą oprócz -2, -1, 0. Warunek dla mianownika pozwala wykluczyć trójki kolejnych liczb parzystych zawierające 0, czyli {-4, -2, 0}, {-2, 0, 2} i {0, 2, 4}. Zauważmy, że z czterech kolejnych liczb naturalnych w liczniku jedna dzieli się przez 3 (bo co trzecia liczba naturalna jest wielokrotnością trójki), dwie inne są parzyste, a jedna z nich dzieli się przez 4 (bo co czwarta liczba naturalna jest wielokrotnością czwórki). Zatem licznik jest podzielny przez 3·2·4=24. Z kolei mianownik przedstawiliśmy jako iloczyn liczby 8 i trzech kolejnych liczb całkowitych. Jedna z nich dzieli się przez 3, więc mianownik jest podzielny przez 8·3=24. Skoro licznik i mianownik są podzielne przez 24, to ułamek jest skracalny przez 24.
Zad. 2. Korzystając z definicji wartości bezwzględnej widać, że wykres tej funkcji składa się z fragmentów wykresów trzech funkcji liniowych:
- dla x<0 jest to y=-2x+3,
- dla 0≤x≤1 jest to y=3,
- dla x>1 jest to y=2x+1.
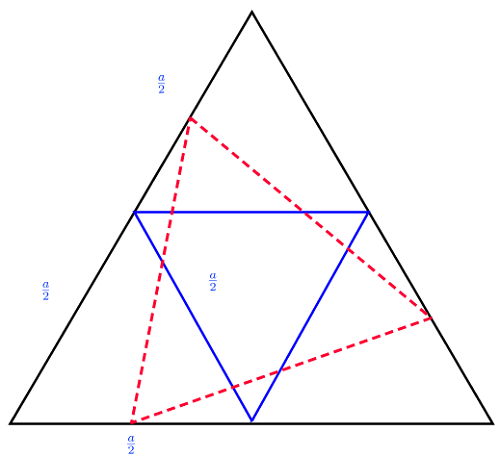
Zad. 3. Wszystkie trójkąty równoboczne są figurami podobnymi. Stosunek długości większego do mniejszego trójkąta opisanego w zadaniu może zawierać się w przedziale (1, 2], zatem stosunek ich pól zawiera się w przedziale (1, 4], bo stosunek pól figur podobnych jest kwadratem skali ich podobieństwa. Gdyby wierzchołki obu trójkątów się pokrywały, stosunek boków byłby równy 1 (ale żaden trójkąt nie byłby wtedy mniejszy, więc ten wypadek wykluczamy). Gdy będziemy przesuwać wierzchołki trójkąta wpisanego po bokach dużego trójkąta w stronę środków tych boków, pole trójkąta wpisanego będzie się zmniejszać, aż stanie się czterokrotnie mniejsze, gdy wierzchołki mniejszego trójkąta będą środkami boków dużego trójkąta (jak na poniższym rysunku). Dalsze przesuwanie wierzchołków mniejszego trójkąta powoduje zwiększenie się jego pola aż do momentu ponownego pokrycia się wierzchołków obu trójkątów i wyrównania się ich pól.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
